Skip to main content

Section 2.6 Vector Addition

Subsection 2.6.1 Graphical Vector Addition

As a typical example across the sections below, consider that two cables are pulling on an eye bolt with forces of \(\vec{A} = \lb{5} \) pointing \(60°\) above the \(x\) axis, and \(\vec{B} = \lb{3} \) acting at a 45° angle below the \(x\) axis. The tension of a cable is the magnitude of the force that the cable applies, and is a scalar.

This diagram shows two forces added together to create a resultant using four different approaches. Change the view slider to see the different interpretations. We will examine the other options in this interactive in the section below. Note that polar coordinates are a better fit when specifying a vectors magnitude and direction, while Cartesian coordinates work better for \(x\) and \(y\) components.

Figure 2.6.1. Vector Addition Methods

There are two ways to graphically add vectors: the Triangle Rule and Parallelogram Rule. Note that in this section we focus on problems where just two vectors are summed to find their resultant. When you need to find the resultant of more than two vectors, it is typically best to use the Algebraic Addition of Components below.

  • For the Triangle Rule, place the tail of one vector at the tip of the other vector, then draw the resultant from the first vector's tail to the final vector's tip.
  • Next for the Parallelogram Rule, you line up the tails of both vectors, then complete a parallelogram with extension lines parallel to each vector. The resultant is equal to the diagonal from the tails to the opposite corner.

Refer to the interactive in Figure 2.6.1. This interactive allows you to adjust the directions of both the \(\lb{5} \) and \(\lb{10}\) tension forces acting on the eye bolt and see how the triangle rule and parallelogram rule both give you the same resultant force \(\vec{R}\text{.}\)

Once you draw your triangle or parallelogram, then you can use various tools from trigonometry to solve for the unknown sides or angles. The triangle definitions can be viewed in Figure 2.6.2 and the trigonometric tools for triangles you need are found in Table 2.6.3 below.

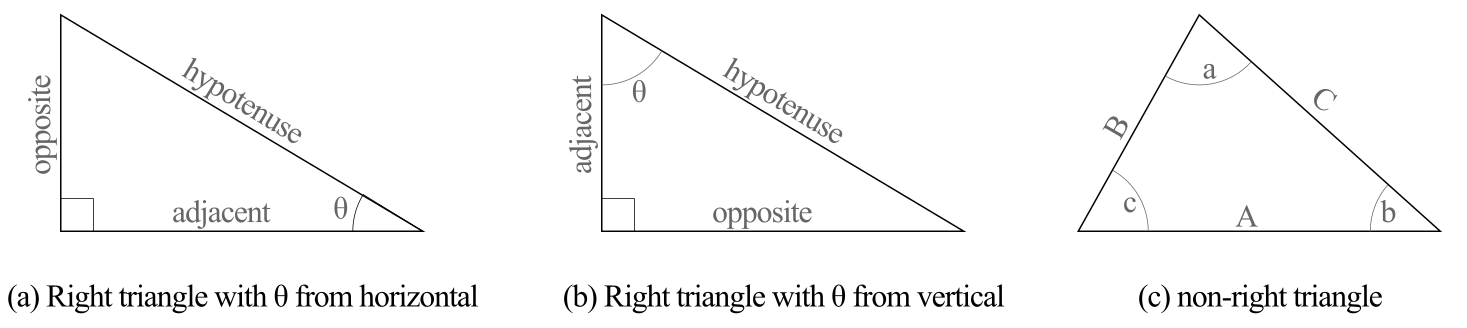
Figure 2.6.2. Definitions of the sides of a right triangle where an angle \(\theta\) is measured from (a) horizontal and (b) vertical. Additionally the sides and angles of a non-right triangle are showin in (c).
Table 2.6.3. Trigonometric tools for solving vector triangles and parallelograms

Right triangle identities
\begin{gather*} \sin \theta = \frac{\rm{Opposite}}{\rm{Hypotenuse}}\\ \cos \theta = \frac{\rm{Adjacent}}{\rm{Hypotenuse}}\\ \tan \theta = \frac{\rm{Opposite}}{\rm{Adjacent}} \end{gather*}

Law of sines Useful for non-right triangles with at least one side + opposite-angle pair.
\begin{equation*} \frac{A}{\sin a} = \frac{B}{\sin b} = \frac{C}{\sin c} \end{equation*}

Where capital letters are the length of triangle sides and lower-case letters are opposing angles as shown in Figure 2.6.2.

Law of cosines Use for non-right triangles when the law of sines doesn't work.
\begin{equation*} C^2 = \sqrt{A^2 + B^2 - 2AB\cos c} \end{equation*}

Where capital letters are the length of triangle sides and lower-case letters are opposing angles as shown in Figure 2.6.2.

Using triangle-based geometry to solve vector problems can be a quick and powerful tool, but includes the following limitations:

  • There are only three sides in a triangle; thus graphical addition is limited to two vectors (and the resultant). You could still draw graphical shapes with three or more vectors to be added but then the shapes become complex polygons.
  • If you fail to draw the correct vector triangle, you will not find the correct answer.
  • The trigonometric functions in Table dd above, are all scalar functions. Thus, they are quick ways of solving for the magnitudes of vectors and the angle between vectors, but you would need to complete more analysis if you were asked to find the vector components of an angle from a given datum.

If any of these limitations apply to the problem you are trying to solve, never fear, just move onto the next section where you will learn to perform the Algebraic Addition of Components.

Subsection 2.6.2 Rectangular Components

One of the most useful tools for solving problems with vector algebra is to express vectors in terms of rectangular components. We can describe any two-dimensional vector as the vector sum of two rectangular components, or three for three-dimensional vectors.

Recall that vector components of arbitrary vector \(\vec{F}\) are the sides of a parallelogram which has \(\vec{F}\) as its diagonal. Because there are an infinite number of such parallelograms, each vector has an infinite number of pairs of components. When the parallelogram happens to be a rectangle, the components are called rectangular components. One particular set of rectangular components is of special interest: when the sides of the rectangle are parallel to the \(x\) and \(y\) axes. These particular components are designated \(\vec{F}_x\) and \(\vec{F}_y\) where the subscripts indicate that the components are aligned with the \(x\) and \(y\) axes.

We can express the Cartesian vector components of \(\vec{F}\) as:

\begin{equation} \vec{F} = \vec{F}_x + \vec{F}_y = \vec{F}_{x'} + \vec{F}_{y'}\tag{2.6.1} \end{equation}

You can express any vector as the sum of two orthogonal components using either a horizontal \(x\) axis and vertical \(y\) axis or rotate the coordinate system to any other angle you like.

One benefit of finding orthogonal vector components is that each component is independent of the other. This independence simplifies the vector computations greatly by allowing us to use independent equations for each orthogonal direction. Another benefit is that once you have separated a vector into vector components parallel to the coordinate axes, you can treat these components as scalar quantities and use ordinary algebra rather than vector algebra to solve many problems.

Subsection 2.6.3 Algebraic Addition of Components

While the parallelogram rule and the graphical and trigonometric methods covered in the previous section are useful tools to for visualizing and finding the sum of two vectors, they are not particularly suited for adding more than two vectors.

Consider vector \(\vec{R}\) which is the sum of several vectors \(\vec{A}\text{,}\) \(\vec{B}\text{,}\) \(\vec{C}\) and perhaps more. We say that \(\vec{A}\text{,}\) \(\vec{B}\) and \(\vec{C}\) are the components of \(\vec{R}\text{,}\) and the \(\vec{R}\) is the resultant of \(\vec{A}\text{,}\) \(\vec{B}\) and \(\vec{C}\text{.}\) It is easy enough to say that \(\vec{R} = \vec{A}+ \vec{B}+ \vec{C}\text{,}\) but how can we calculate \(\vec{R}\) if we know the components? You could draw the vectors arranged tip-to-tail and then use the triangle rule to add the first two components, then use it again to add the third component to that sum, and so forth until all the components have been added. The final sum is the resultant, \(\vec{R}\text{.}\) The process gets progressively more tedious the more components there are to sum.

This section introduces an alternate method to add multiple vectors which is straightforward, efficient and robust. This is called algebraic method, because the vector addition is replaced with a process of scalar addition of scalar components. The algebraic technique works equally well for two and three dimensional vectors, and for summing any number of vectors.

To find the sum of multiple vectors using the algebraic:

  1. Find the scalar components of each component vector in the \(x\) and \(y\) directions using the P to R procedure described in Subsection 2.3.3.
  2. Algebraically sum the scalar components in each coordinate direction. The scalar components will be positive if they point right or up, negative if they point left or down. These sums are the scalar components of the resultant.
  3. Resolve the resultant's components to find the magnitude and direction of the resultant vector using the R to P procedure described in Subsection 2.3.3.

This process is illustrated in the following interactive diagram and in the next example.

Figure 2.6.4.

We could write the equation for the resultant force \(\vec{F}_R\)

\begin{equation*} \vec{F}_R = \sum F_x \ihat + \sum F_y \jhat + \sum F_z \khat \end{equation*}

or in bracket notation

\begin{equation} \vec{F}_R = \left \langle \Sigma F_x,\Sigma F_y,\Sigma F_z\right \rangle \tag{2.6.2} \end{equation}

The interactive diagram in Figure 2.6.1 demonstrates this method. When you move the slider to the Rectangular Components position you will forces \(\vec{A}\) and \(\vec{B}\) resolved into components, which are then added together to find the components of the resultant force \(\vec{R}\text{.}\)

Example 2.6.1. Example.

Given some vectors, find their resultant using the algebraic method

Answer

Solution

Set up a table, etc.

This interactive allows you to input the three-dimensional vector components of forces \(\vec{A}\) and \(\vec{B}\) and view the resultant force \(\vec{R}\) which is the sum of \(\vec{A}\) and \(\vec{B}\text{.}\)

Figure 2.6.5. Vector Addition in Three Dimensions

Subsection 2.6.4 Vector Subtraction

Like one-dimensional vector subtraction, the easiest way to handle two dimensional vector subtraction is a combination of taking the negative of a vector followed by vector addition. Multiplying any vector by -1 preserves its magnitude but flips its direction, having the net effect of changing the sign of each scalar component. After flipping the vector you are subtracting, then you can choose any of the above techniques for vector addition.