Section 2.8 Cross Products
The vector cross product is a mathematical operation applied to two vectors which produces a third vector as a result. It's sometimes called the vector product, to emphasize this and to distinguish it from the dot product which produces a scalar value. The \(\times\) symbol is used to indicate this operation. The interactive shows the relation of the cross product to the two vectors and the angle between them.
The cross product is defined by
where \(A\) and \(B\) are the magnitudes of \(\vec{A}\) and \(\vec{B}\text{,}\) \(\theta\) is the angle between them, and \(\hat{\vec{u}}\) is a unit vector perpendicular to the plane of \(\vec{A}\) and \(\vec{B}\) whose sense is determined with the right hand rule.
The magnitude of vector \(\vec{C}\) is is the area of the parallelogram formed by vectors \(\vec{A}\) and \(\vec{B}\text{.}\) The magnitude of the cross product is zero if \(\vec{A}\) and \(\vec{B}\) are parallel, and it is a maximum when they are perpendicular.
You will notice that all the terms in the cross product equation are quite similar to those of the dot product, with the exception of the unit vector \(\hat{\vec{u}}\) and the use of \(\sin\) rather than \(\cos\text{.}\) This unit vector \(\hat{\vec{u}}\) is simple to find in a two-dimensional problem as it will always be perpendicular to the page, but for three-dimensional cross products it is advisable to use a vector determinate method discussed here.
Cross Product of Unit Vectors.
Since unit vectors have a unit magnitude by definition, and orthogonal vectors are perpendicular to each other, the magnitude of the cross product of two different unit vectors will always be one. The direction is given by the cross product circle shown in Figure 2.8.1. For example when you cross \(\ihat\) with \(\jhat\) you are going in the positive direction (counterclockwise which is also the + RHR direction) around the blue inner circle and thus the answer is \(+\khat\text{.}\) But when you cross \(\jhat\) into \(\ihat\) you go in the negative (clockwise) direction around the circle and thus get a \(-\khat\text{.}\) Remember that the order of cross products matter. If you put the vectors in the wrong order, you will introduce a negative value error.
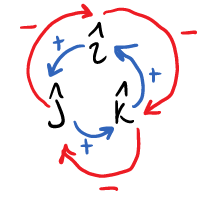
All the possible combinations of positive value unit vector cross products create the following equations
If you have any negative unit vectors it is easiest to separate the negative values until after you have taken the cross product. Therefore
Cross Product of Arbitrary Vectors.
The cross product of two three-dimensional vectors can be calculated by evaluating the determinant of this \(3\times 3\) matrix.
Here, the first row are the unit vectors, the second row are the components of \(\vec{A}\) and the third row are the components of \(\vec{B}\text{.}\)
Calculating the \(3 \times 3\) determinant can be reduced to calculating three \(2 \times 2\) determinants using the method of cofactors, as follows
Finally a \(2 \times 2\) determinant can be evaluated with the formula
In practice, the easiest way to evaluate a three dimensional cross product is to use the augmented determinant below, where the first two columns have been copied and placed after the determinant. The cross product is then calculated by adding the product of the red diagonals and subtracting the product of blue diagonals.
In two dimensions, vectors \(\vec{A}\) and \(\vec{B}\) have no \(z\) components, so (2.8.2) reduces to
This equation produces the same result as equation (2.8.1) and you may use it if it is more convenient.
Example 2.8.1. 2-D Cross Product.
Determine the cross product \(\vec{A} \times \vec{B}\text{.}\)
In this solution we will apply equation (2.8.1).
The direction of the the cross product is determined by applying the right hand rule. With the right hand, rotating \(\vec{A}\) towards \(\vec{B}\) we find that our thumb points into the \(xy\) plane, so the direction of \(\hat{\vec{u}}\) is \(-\khat\text{.}\)
From the diagram:
From (2.8.6):
Example 2.8.2. 3-D Cross Product.
Find the cross product of \(\vec{A} = \langle 2,4,-1 \rangle \) and \(\vec{B} = \langle 10, 25, 20 \rangle\text{.}\) The components of \(\vec{A}\) are in meters and \(\vec{B}\) are in Newtons.
To solve, set up the augmented determinant and evaluate it by adding the left-to-right diagonals and subtracting the right-to-left diagonals. (2.8.5).
Given:
Use the embedded Sage calculator to find the cross product or check your work.
\(\vec{A}\) and \(\vec{B}\) are defined in the first two lines, and A.cross_product(B) is the expression to be evaluated. Click Evaluate to see the result. You'll have to work out the correct units for yourself.
Try changing the third line to B.cross_product(A). What changes?