Section 1.1 Introduction
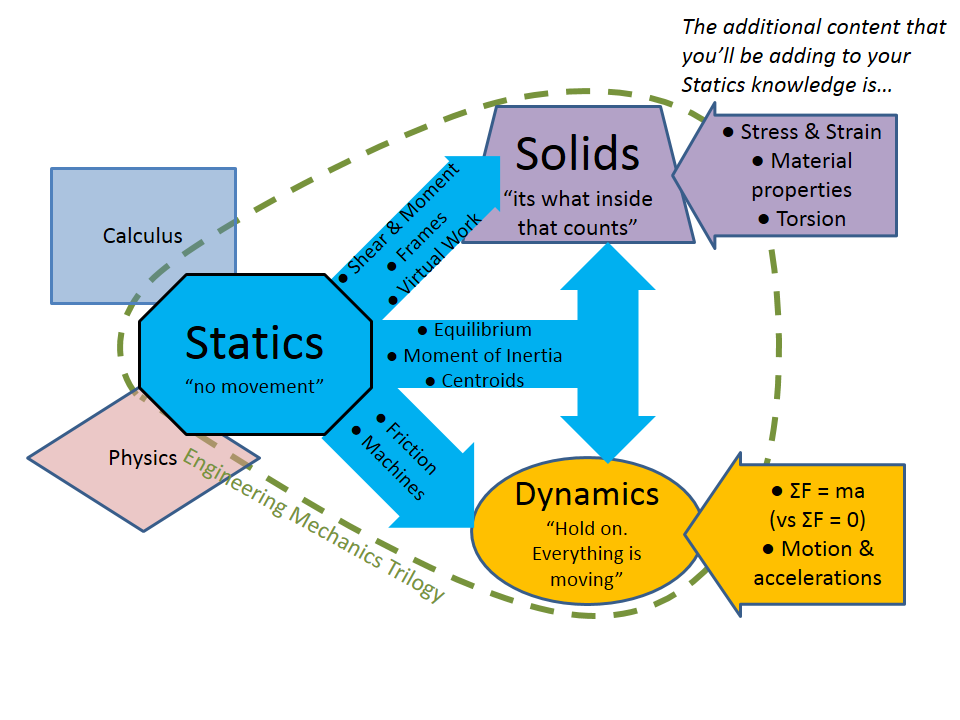
Engineering Statics is the gateway course into the rest of engineering mechanics, which is the application of Newtonian physics to design and analyze objects, systems, and structures with respect to motion, deformation, and failure. In addition to learning about the subject itself, you will also develop your skills in the art and practice of problem solving and mathematical modeling, skills which will benefit you throughout your engineering career.
The course is called “Statics” because we are concerned with particles and rigid bodies which are in equilibrium, and these will usually be stationary i.e., static.
The chapters in this book cover:
- Introduction
overview of statics and an introduction to units and problem solving
- Forces and Other Vectors
basic principles and mathematical operations of force and position vectors
- Equilibrium of Particles
vector tools on particle equilibrium problems
- Moments and Resultants
the rotational tendency of forces, called moments and summarizing total loading with resultants
- Equilibrium of Rigid Bodies
balancing of forces and moments for single rigid bodies
- Equilibrium of Structures
balancing of forces and moments on interconnected systems of rigid bodies
- Properties of Shapes
the center of mass and area moment of inertia
- Internal Loading within Rigid Bodies
finding internal forces and moments in rigid bodies
- Friction
equilibrium of bodies subject to friction
- Virtual Work
an alternate equilibrium methodology based upon the product of applied loads and displacement
Your statics course may not cover all of these topics, or choose to move through them in a different order. You will find examples of some of the problem types you will learn to solve below.
Below are two examples of equilibrium problems you’ll learn to solve in statics. Notice that each can be described with a picture and problem statement, a free-body diagram, and equations of equilibrium.

A person on a slackline weighs \(\lb{140}\text{.}\)
If angles \(\alpha\) and \(\theta\) are known, find the tension is in each end of the slackline.
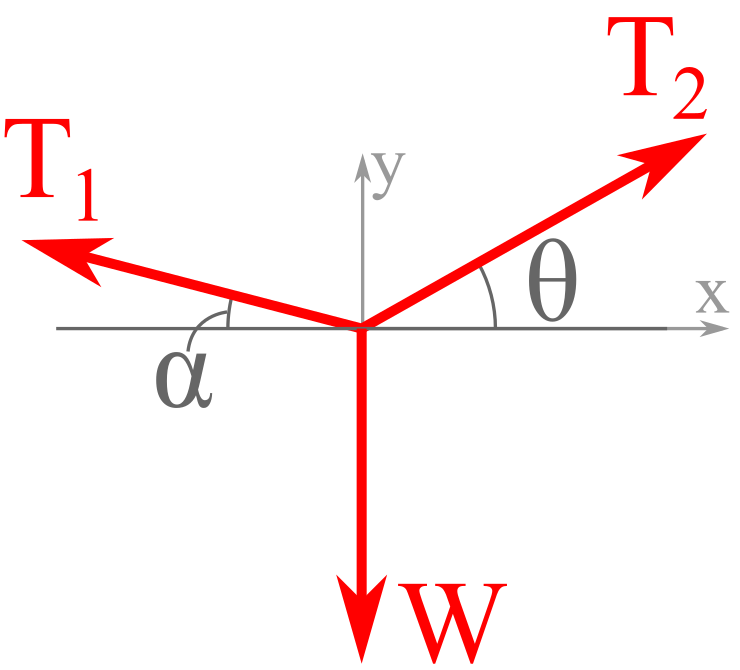
Person’s point of contact to slackline:
Given the interaction forces at point \(C\) on the upper arm of the excavator, find the internal axial force, shear force, and bending moment at point \(D\text{.}\)

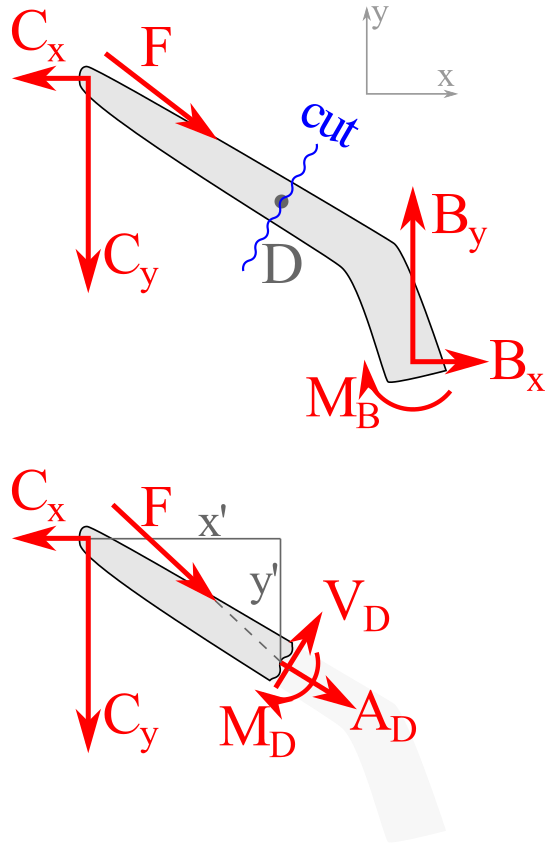
Section cut FBD:
The knowledge gained in Statics will then flow into other engineering mechanics topics of Dynamics, Mechanics of Solids, also commonly called Strength or Mechanics of Materials, and Fluid Mechanics. The skills you learn in Statics will be a foundation of your academic career.