Section 5.4 Solution Strategies
There are many sets of independent equations which you are able to use to solve two-dimensional equilibrium problems. The most typical set of equations used are:
If you choose this typical set of equations, you have two decisions to make to help decrease the amount of math you need to solve for the unknowns. First, choose an axis system. To decrease the number of terms in the \(\Sigma \vec{F}_x\) and \(\Sigma \vec{F}_y\) equations, pick an axis system that lines up with as many unknown force vectors as possible. Second, you can sum moments around any point on or off the body, so try to select:
- a point at the intersection of as many force lines-of-action as possible, and
- a point which minimizes the number of unknowns in your moment equation.
Sometimes the two factors will optimize the same point. Other times, there are compromises to make. Do not sweat these two decisions too hard in the beginning; the selection of any axis and any point to sum moments around will give you the same answer.
The typical choice of equations stated above are certainly not the only set of equations that can be used. Any force equations can be replaced with a linearly independent moment equation, so the other possibilities are:
- The typical choice, two equations summing forces in perpendicular directions and one moment equation.\begin{align*} \Sigma\vec{F}_x\amp=0 \amp\Sigma\vec{F}_y\amp=0 \amp\Sigma\vec{M}_o\amp=0\text{, or} \end{align*}
- two moment equations and force equation. This choice is used for equilibrium involving parallel forces.\begin{align*} \Sigma\vec{F}_x\amp=0 \amp\Sigma\vec{M}_A\amp=0 \amp\Sigma\vec{M}_B\amp=0\text{, or} \end{align*}
- three moment equations, such as\begin{align*} \Sigma\vec{M}_A\amp=0 \amp\Sigma\vec{M}_B\amp=0 \amp\Sigma\vec{M}_C\amp=0\text{.} \end{align*}The three points chosen must not be collinear, i.e. they must not all lie on the same straight line.
While following one of the three rules above does guarantee the independence of your equations, you have further freedom to choose equations that help you to find efficient solutions. Efficiency, in this case, is defined as the desire to avoid simultaneous equations when possible. This efficiency is based on the fact that equations with only a single unknown are faster to solve than multiple-unknown equations that require substitution, linear algebra, or other solution techniques. The four choices which contribute to setting up efficient equations are the selection of 1) equilibrium equations, 2) the axis, 3) the points you sum moments around, and finally, 4) the order in which you solve the equations.
Consider the L-shaped body supported by a roller on the left end and a pin on the lower right end shown in the diagram. The body supports a horizontal force applied at the elbow and a constant-value torsional couple-moment on the left end.
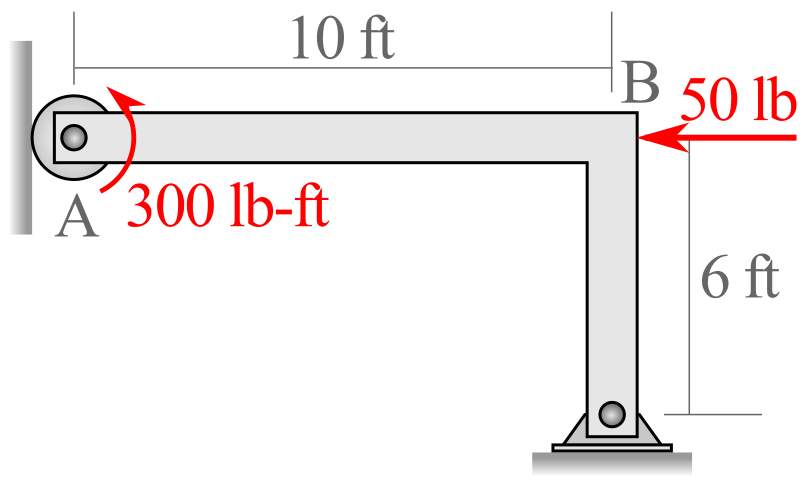
Following the five steps to create a free-body diagram (isolate, axis, load, support, and dimension) we can create the free-body diagram shown here. Notice that there are three unknowns which we will solve for using equations of equilibrium.
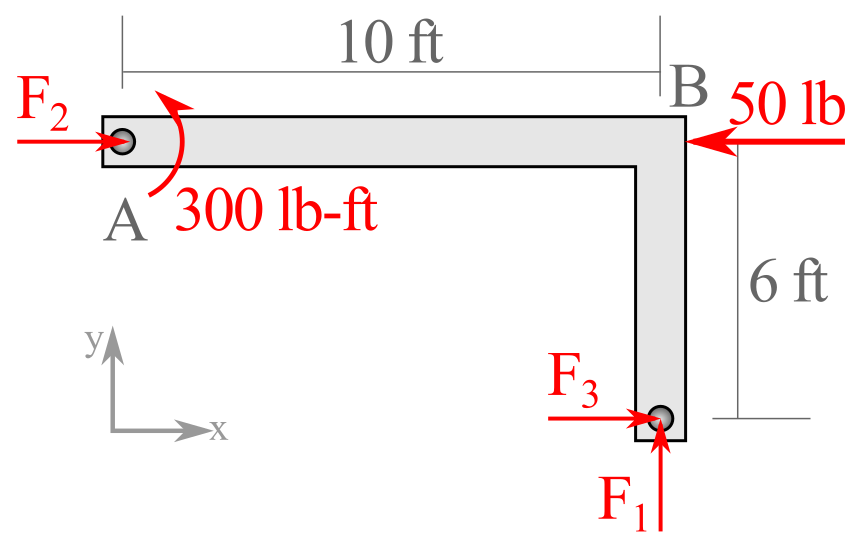
Some equations of equilibrium are simpler to solve than others. If an equation yields only a single unknown, it is a good starting point as multiple-unknown / multiple-equations sets can take more effort to solve, especially under the stress of a quiz or exam. The equations below are all valid equilibrium equations that could serve as a starting point for your computations.
Note that we have written six equations to show the breadth of possibilities, but when you solve two-dimensional equilibrium problems, you are limited to three independent equations. Selecting more equations does not give you more information, it only confirms what you already knew, like \(0 = 0\) or \(A_x = A_x\text{.}\) Once you have selected your three equations, the free-body diagram is now represented in equation form to enable you to solve for unknowns present on the free-body diagram.
The signs (\(\pm\)) of all known and unknown terms in your equations of equilibrium come from the axis system you draw as part of your free-body diagram. The only exception to this rule in the set above is the equation \(\nearrow_+ \vec{F}_{45^{\circ}}= 0\) which is essentially defining an additional axis at \(\ang{45}\) above horizontal.
The steps in Table 5.4.1 below walk through the second of the three options for independent equation sets: three moment equations not involving three co-linear points. This option turns out to be an efficient solution pathway for this system. Step 1 will sum moments around point \(B\text{,}\) yielding a single unknown —\(F_3\text{.}\) Step 2 sums moments around point C to solve for \(F_2\text{.}\) Step 3 sums moments around point A to solve for \(F_1\text{.}\) Finally, Step 4 (optional) draws the free-body diagram with all forces presented in the correct direction.
Step |
Questions to ask yourself |
Computations and Discussion |
Step 1 |
Q: Which equations of equilibrium give me the fewest unknown values? |
\begin{align*}
\Sigma \vec{M}_B \amp =0\\
+\ftlb{300} + (\ft{6})F_3 \amp =0\\
F_3\amp =\lb{-50}
\end{align*}
|
A: Summing forces in the \(y\) direction or summing moments about points \(B\) or \(C\text{.}\) Selected \(\Sigma \vec{M}_B=0\) |
Note that the negative value of \(F_3\) let us know that the correct direction (\(\leftarrow\)) was opposite the hypothesized direction in our free-body diagram. |
|
| Step 2 | Q: Is there another equation of equilibrium that only has one unknown? |
\begin{align*}
\Sigma \vec{M}_C \amp =0\\
+\ftlb{300}+ (\ft{6})\lb{50} - (\ft{6})F_2 \amp =0\\
F_2\amp =\lb{+100}
\end{align*}
|
A: Summing forces in the \(y\)-direction or summing moments about point \(A\) or \(B\text{.}\) Selected \(\mathbf{\Sigma \vec{M_C}=0}\) |
Note that the positive value of \(F_2\) confirms that we assumed the correct direction (\(\rightarrow\)) on our free-body diagram. |
|
| Step 3 | Q: Which equations of equilibrium give me the fewest unknown values? |
\begin{align*}
\Sigma \vec{M}_A \amp =0\\
+\ftlb{300} -(\ft{6})\lb{50}+ (\ft{10})F_1 \amp =0\\
F_1\amp =0
\end{align*}
|
A: Summing forces in the \(y\)-direction or summing moments about points \(A\) or \(B\text{.}\) Selected \(\mathbf{\Sigma \vec{M_A}=0}\) |
Note that this is the same value we would have found if we had summed forces in the \(y\) direction \(\Sigma \vec{F}_y=0\text{.}\) |
|
Step 4 optional |
Q: Do the direction and magnitude of the final vectors make sense? |
see the figure below. |
A: Yes, the final values all seem to make sense: 1) the sum of the horizontal forces is zero, 2) there are no vertical forces, and 3) summing the moments about either \(B\) or \(C\) gives a net moment of zero. |
Result: L-shaped object with all unknown forces determined.
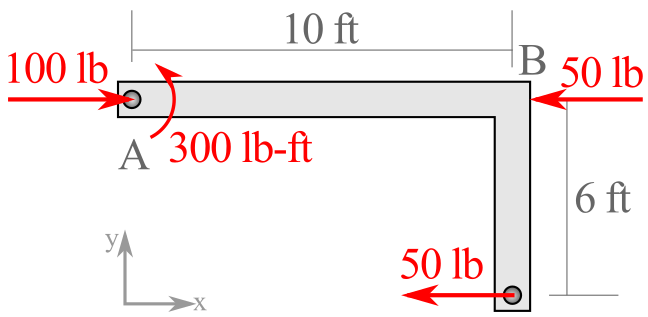
Notice that to solve for the three unknowns that we summed moments about \(A\text{,}\) \(B\text{,}\) and \(C\text{.}\) Each equation was efficient — yielding a single unknown. The same solutions could have been found with any other set of equations following the three rules shared previously. If you choose another equation that has not already been used, you will end up checking our solutions. In the case of \(\Sigma \vec{F}_x=0\) we would find that \(\lb{100}-\lb{50}-\lb{50}=0\) which confirms that our solutions are accurate.
As a reflection, the equations below show several different starting strategies for solving this problem.
It's worthwhile to think ahead about your choice of equilibrium equations and select a set which will make the mathematics easier. Here are some possible strategies for solving this example.
| Equation Set | Unknowns | Strategy |
\begin{equation*}
\begin{cases}
①\; \Sigma F_x = 0\\
②\; \Sigma F_y = 0\\
③\; \Sigma M_C = 0
\end{cases}
\end{equation*}
|
\begin{gather*}
F_1, F_3\\
F_2\\
F_1
\end{gather*}
|
1. Solve \(③\) for \(F_1\text{.}\)\(\\\) 2. Solve \(②\) for \(F_3\text{.}\)\(\\\) 3. Solve \(①\) for \(F_2\text{.}\) |
\begin{equation*}
\begin{cases}
①\; \Sigma M_B = 0\\
②\;\Sigma M_C = 0\\
③\; \Sigma F_y = 0
\end{cases}
\end{equation*}
|
\begin{gather*}
F_3\\
F_1\\
F_2
\end{gather*}
|
1. Solve \(①\) for \(F_3\text{.}\)\(\\\)2. Solve \(②\) for \(F_1\text{.}\)\(\\\)3. Solve \(③\) for \(F_2\text{.}\) |
\begin{equation*}
\begin{cases}
①\; \Sigma F_x = 0\\
②\;\Sigma M_A = 0\\
②\; \Sigma M_D = 0
\end{cases}
\end{equation*}
|
\begin{gather*}
F_1, F_3\\
F_2, F_3\\
F_1, F_3
\end{gather*}
|
1. Solve \(2 \times 2\) system of equations,\(\){\(①, ③\)}, for \(F_1\) and \(F_3\text{.}\)\(\\\) 2. Use result in \(②\) to find \(F_3\text{.}\) |
\begin{equation*}
\begin{cases}
①\; \Sigma M_O = 0\\
②\;\Sigma M_A = 0\\
②\; \Sigma M_D = 0
\end{cases}
\end{equation*}
|
\begin{gather*}
F_1, F_2\\
F_2, F_3\\
F_1, F_3
\end{gather*}
|
Solve \(3 \times 3\) system of equations,\(\){\(①\text{,}\) \(②\text{,}\) \(③\)} for \(F_1\text{,}\) \(F_2\) and \(F_3\text{.}\) |