Section 5.1 Free Body Diagrams
Key Questions
At the end of this chapter you should be able to answer these questions.
- What are the five steps to create a free-body diagram?
- What are degrees of freedom, and how do they relate to stability?
- Which reaction forces and couple-moments come from each support type?
- What are the typical support force components and couple-moment components which can be modeled from the various types of supports?
Free body diagrams are the tool that engineers use to identify the forces and moments that influence an object. They will be used extensively in statics, and you will use them again in other engineering courses: Dynamics, Kinematics, Strength of Materials, and Fluid Mechanics, so your effort to master them now is worthwhile. Although the concept is simple, students often have great difficulty with them.
Their importance can't be overstated. They are the basis for writing all equilibrium equations; if your free-body diagram is incorrect your equations, analysis, and solutions will be wrong as well.
You are required to draw and label a free-body diagram for every equilibrium problem
Creating Free Body Diagrams.
Drawing correct free-body diagrams is the single most important step for solving equilibrium problems. You are encouraged to find a repeatable process for creating them. We suggest following these five steps.
-
Isolate.
The “free-body” in free-body diagram means that the body to be analyzed must be free from the supports that are physically holding it in place. Sketch an outline of the object as if it is floating in space. To reiterate, do not draw free-body diagram forces on top of your problem drawing — the body needs to be drawn free of its support for a free-body diagram to be created.
-
Axis.
Establish a right-hand coordinate system to use as a reference for your equilibrium equations. Any right-hand system works, but look ahead and select one which minimizes the number of unknown force components in your equations. The choice is technically arbitrary, but a good reference system should help you solve the problem. If you and another student pick different reference systems, you should both get the same answer, while expressing your work with different components.
-
Loasd.
Add vectors representing the applied forces and couple moments acting on the body. Include the body's weight if it is available. Every vector should have a descriptive variable name and a clear arrowhead indicating its direction. If a vector’s direction is unknown, you must assume one.
-
Reactions.
Traverse the perimeter of the object and replace the supports removed by isolating the body with equivalent forces and couple moments (collectively reactions) provided to the body. There are two ways to find the reactions from supports:
- Supports provide the type (force or moment) and direction of support a body needs to resist applied loads
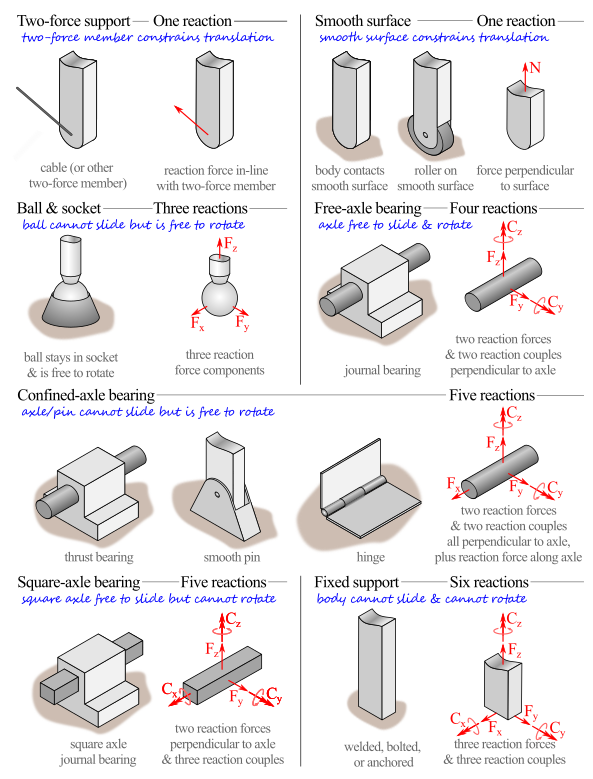
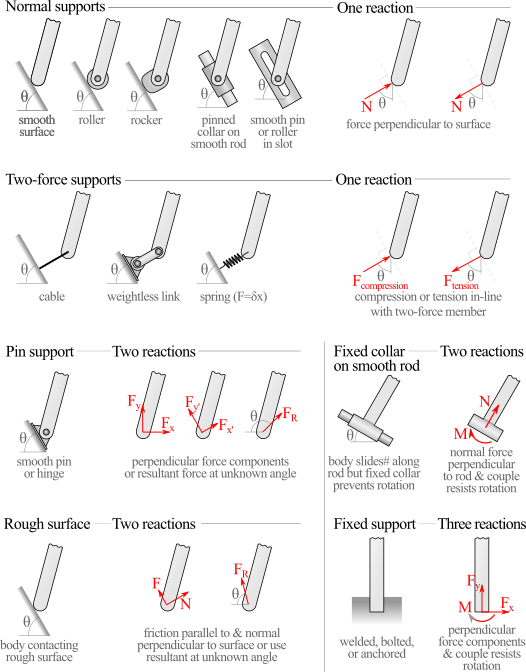
- Each support type provides a limited set of possible reactions as shown in Figure 5.1.1.
Interpreting the correct reaction forces and couple moments coming from supports is perhaps the most challenging step in the entire equilibrium process. Label each reaction with a descriptive variable name and a clear arrowhead. Again, if a vector's direction is unknown just assume one.
-
Dimensions.
Give all pertinent dimensions and angles on the free-body diagram, but don't clutter it up with unneeded information; supply only the dimensions and angles you need for your calculations. This diagram should be a “stand-alone” presentation.
Drawing good free-body diagrams is surprisingly tricky and requires practice. Study the examples, think hard about them, do lots of problems, and learn from your errors.
Two-dimensional Reactions.
Supports supply reaction forces and moment which prevent bodies from moving when loaded. In the most basic terms, forces prevent translation, and moments prevent rotation. As you learned in Chapter 4, there are two types of moments, couple-moments and \(\vec{r} \times \vec{F}\) moments both of which can prevent rotation.
The reactions a support supplies depends on the nature of the particular support. For example, a door hinge allows the door to rotate freely but prevents it from moving left, right, up, or down. We model a hinge as having horizontal and vertical reaction forces, but no reaction moment around the pin. We can evaluate all the other physical supports in a similar way to come up with the table below. You will notice that some two-dimensional supports only restrain one degree of freedom and others restrain up to three degrees of freedom. The number of degrees of freedom directly correlates to the number of unknowns created by the support.
The table below shows typical two-dimensional support methods and the corresponding reaction forces and moments supplied each.
Three-dimensional Reactions.
The main added complexity with three-dimensional objects is that there are more possible ways the the object can move, and also more possible ways to restrain it. The table below show the types of supports which are available and the corresponding reaction forces and moment. As before, your free-body digrams should show the reactions supplied by the constraints, not the constraints themselves.