Section 5.6 Stability and Determinacy
Key Questions
At the end of this chapter you should be able to answer these questions.
- What does stable mean for a rigid body?
- What does determinant mean for a rigid body?
- Does stability a depend on the external loads or only the reactions?
- How can I tell if a system is determinate?
- How can I decide if a problem is both stable and determinate, which makes it solvable statics?
Many equilibrium problems cannot be solved by the methods we are now learning, and it is fruitless to try. This section will help you learn how to separate the solvable problems from the unsolvable ones 1 .
A body in equilibrium is held stable by supports that both counteract the applied loads and also restrict the body’s motion. The number and orientation of the support components determine if a rigid body is stable or unstable. You have also learned to represent supports with reaction forces and couple-moments on a free-body diagram and to create equations from a free-body diagram to solve for the unknown terms. Having enough information in these equations to mathematically solve a statics problem determines if the problem is either determinate or indeterminate. All problems in statics need to be determinate and stable. In subsequent courses, you will learn additional tools/equations to evaluate more complicated systems. The next two sections drill down into these terms a bit deeper.
Stable vs. Unstable.
When the support components are sufficient to restrain a body from moving, we say that the body is stable. The stability of a two-dimensional body is ensured when the body is prevented from 1) translating in the plane of the page and 2) rotating around an axis perpendicular to the page. If the supports do not allow a body to move, we call it stable. Stability is loading independent i.e. the stability of a body is not related to the applied loads. Equilibrium must be maintained for any loading condition.
Determinate vs Indeterminate.
A static system is determinate if the reactions can be found by the methods of statics, that is, by using equilibrium equations.
In order for a system to be determinate, the number of reaction components must equal the degrees of freedom of the body. In terms of forces and moment equations, the number of unknowns (often reaction forces and moments) equals the number of independent equations of equilibrium. For two-dimensional systems, there are three degrees of freedom . Therefore we can determine no more than three unknown reaction components.
An indeterminate system with fewer reaction components than degrees of freedom is under-constrained and therefore unstable. On the other hand, if there are more reaction components than degrees of freedom, the system is both over-constrained and indeterminate.In terms of force and moment equations, the there are more unknowns than than equilibrium equations and so they can't be determined. This is not to say that it is impossible to find the reaction force on an over-constrained system, just that you will not be learning how to find them in this course.
Rules to Validate a Stable and Determinate System.
There are three rules to check if a system is both stable and determinate. While, the rules below can technically be checked in any order, they have been sorted from the quickest to the most time consuming to speed up your analysis.
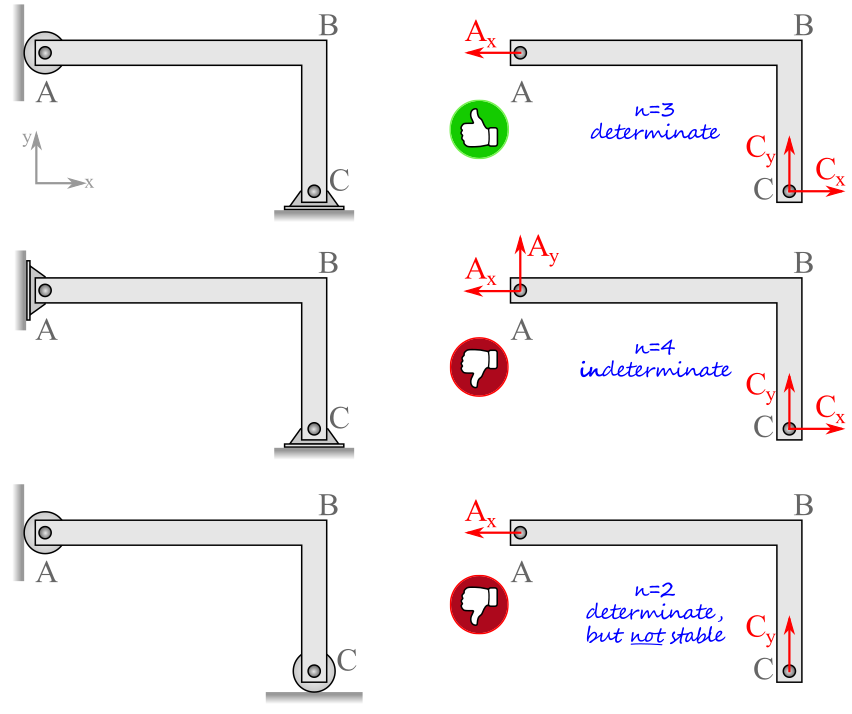
Rule 1:
Are there exactly three reaction components on a two-dimensional body?
If YES, the system is determinate.
If NO, the system is indeterminate or not stable (see rules below).
Rule 2:
Are any reaction force components parallel to one another?
If YES, the system is unstable for translation.
If NO, the system is stable for translation.
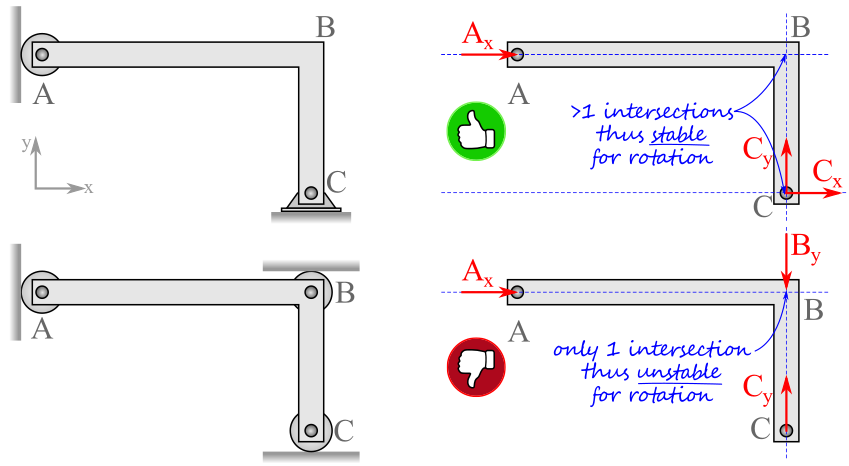
Rule 3:
Do the lines of action of the reaction forces intersect at a single point?
If YES, the system is unstable for rotation about the single intersection point.
If NO, the system is stable for rotation.
