Section 5.7 Three-dimensional Equilibrium
Key Questions
At the end of this chapter you should be able to answer these questions.
- What are the similarities and differences between solving two-dimensional and three-dimensional equilibrium problems?
- Why are some three-dimensional reaction couple-moments “available but not engaged”?
- What kinds of problems are solvable using linear algebra?
Three-dimensional Equilibrium.
To start this section, it is valuable to recognize the similarities and differences between two-dimensional and three-dimensional equilibrium problems. The first similarity is that the general equilibrium equations are the same.
Given that each of the force and moment equations must be solved in each of the three directions, the full set of equations is:
The remaining similarities and differences are contrasted in the XREF table below.
| Two-dimensional | Three-dimensional | ||
| free-body diagram required? | Yes | Yes | |
| forces | in \(x,y\) | in \(x,y,z\) | |
| moments | only about \(z\) | about \(x,y,z\) | |
| degrees of freedom | 3 | 6 | |
| find components with | sin and cos of angles | unit vectors | |
| find moments by | multiplying components | taking vector cross-products | |
| solve equations with | basic algebra or substitution | often use linear algebra |
The general procedure of analysis is exactly the same, only differing in the number of equations to be solved. As there are many similarities between two-dimensional and three-dimensional equilibrium problems, this section briefly points out the similarities and spends more time on the differences.
Non-engaged Reaction Couples.
One new issue we have to face in three-dimensional problems is that some reaction couples are available but not engaged. Before we get into the details for reaction couples, let us discuss what we mean by the word engaged. Picture a crate sitting at rest on a horizontal surface. If you were to attach a cable to the top of the crate, but not pull on the cable, the tension in the cable would be available but not engaged in this condition. Instead, the floor’s normal force would be supporting the full weight of the crate without need of the tension force in the cable. If we were to remove the floor under the crate, then the cable’s tension force would be engaged to support the weight of the crate.
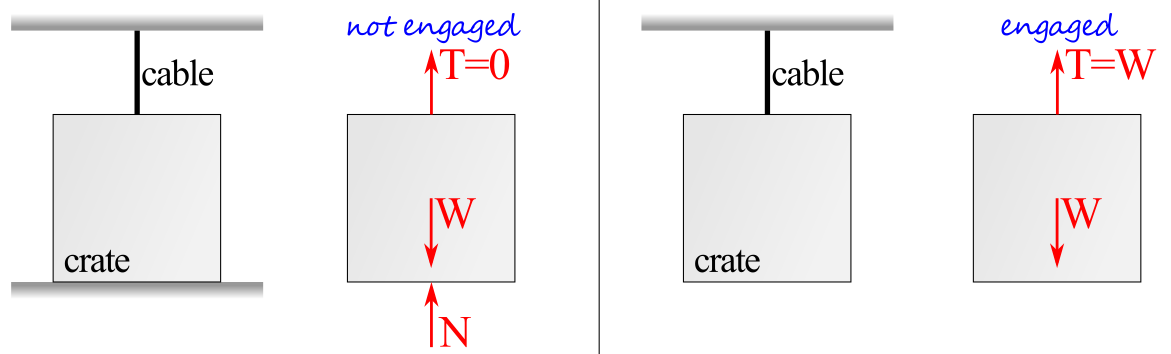
Now lets refocus our discussion on reaction couples and talk through a quick experiment that you can do.
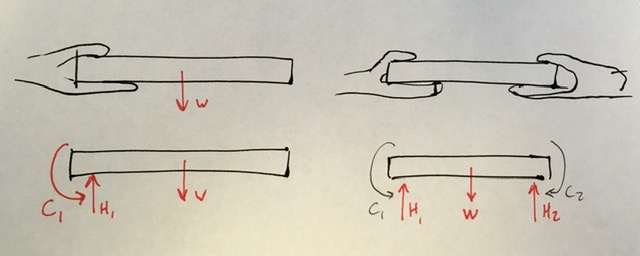
- Find a rigid object around 1 to 3 feet long that you can pick up with one hand. An umbrella, baseball bat, or even a textbook would work.
- Grip the object on one end with one hand. Describe the type of forces and couple-moments you feel in your hand. What would a free-body diagram of the object look like?
- Now grip the object with two hands on either end of the object. How did the forces and couple-moments change from when you were holding with one hand?
You should have discovered that the vertical force from each of your two hands was half of the vertical force required with one hand. But hopefully, you noticed something more than a change in force magnitude. When holding the object with one hand, did you feel that your hand needed to provide a resistance to the rotation of the object? When you grabbed the other side with your second hand, this resistance to rotation was no longer needed. The phenomena that you (hopefully) just discovered can be described by the saying “reaction forces engage before reaction couple-moments”. Essentially, the vertical force in your second hand engaged instead of the couple-moment resistance in your first hand. The reaction couple-moments from both hands are technically both available, but the vertical forces from the other hand engage first, as seen in the XREF Figure below.
Strategies to Solve Three-dimensional Equilibrium Problems.
While three-dimensional systems are closer to reality than their two-dimensional cousins, they do require a bit more math to solve. The two reasons more math is required is:
- The forces and moments require more effort to resolve into components.
- There are more unknown terms and degrees of freedom for each body. Three-dimensional free-body diagrams have up to six as compared to only three for two-dimensional systems.
Resolving Forces and Moments into Components.
To break two-dimensional forces into components, you likely used right-triangle trigonometry, sine and cosine. However, three-dimensional forces will likely need to be broken into components using XREF Ch 2 unit vectors.
When summing moments, make sure to consider both the \(\vec{r}\times\vec{F}\) moments and also the couple-moments with the following guidance:
First, choose any point in the system to sum moments around.
-
There are two general methods for summing your \(\vec{r}\times\vec{F}\) moments. Both techniques will give you the same set of equations.
-
Sum moments around each axis.
For relatively simple systems with few position and force vector components, you can find the cross product for each non-parallel position and force vector pair. Using this method requires you to resolve the direction of each cross product pair using the right-hand rule as XREF covered in Ch 4. Recall that there are up to six pairs of non-parallel components that you need to consider.
-
Sum all moments around a point using vector determinates.
Choose a point in the system which is on the line of action of as many forces as possible, then set up each cross product as a determinant. After computing the components coming from each determinant, combine the \(x\text{,}\) \(y\text{,}\) and \(z\) terms into each of the \(\Sigma\vec{M}_x=0\text{,}\) \(\Sigma\vec{M}_y=0\text{,}\) and \(\Sigma\vec{M}_z=0\) equations.
-
Finally, add the components of any couple moments into the corresponding \(\Sigma\vec{M}_x=0\text{,}\) \(\Sigma\vec{M}_y=0\text{,}\) and \(\Sigma\vec{M}_z=0\) equations.
Solving for unknown values in equilibrium equations.
Once you have your \(\Sigma\vec{F}=0\) and \(\Sigma\vec{M}_o=0\) equations in each of your \(x\text{,}\) \(y\text{,}\) and \(z\) directions set up, you could be facing up to six equations and six unknown values. Nearly all equation sets are solvable with substitution, but it can often be easier to solve these large equation sets with linear algebra. Note that the adjective “linear” specifies that your unknown values must be linear terms, which means that each unknown variable cannot be raised to a exponent, be an exponent, or buried inside of a \(sine\) or \(cosine\) function. Luckily, most unknowns in equilibrium are linear terms, except for unknown angles. If you are not familiar with the use of linear algebra matrices to simultaneously solve equations, search the internet for Solving Systems of Equations Using Linear Algebra and you will find plenty of resources.
No matter how you choose to solve for the unknown values, any numeric values which come out to be negative reveal that your initial hypothesis of that vector’s direction was incorrect.
Three-dimensional Equilibrium Examples
(to be added)