Section 9.3 Slipping vs. Tipping
Key Questions
At the end of this chapter you should be able to answer these questions.
- Interpret all the ways that a system could reach impending motion and create free-body diagrams for each scenario
- Select a criterion which you can compare across motion scenarios
- Compare your results to conclude which scenario would reach impending motion first
Application: Failure in Engineering.
Engineering design is trying to forecast (and plan for) all the ways that something can fail. Hence, one of the significant challenges of engineering is knowing what questions to ask and data to gather, to model and design for all the possible failure types. Furthermore, the failure type which occurs at the highest load is not the controlling failure; instead, the system will fail at the lowest load.
This section on friction simulates the same type of process, but instead of focusing on failure, it focuses on the various ways a rigid body can reach impending motion. As shown in [provisional cross-reference: FF] below, imagine a box sitting on a rough surface. Now imagine that we start pushing on the side of the box. Initially, the friction force will resist the pushing force, and the box will sit still. As we increase the force pushing the box, however, one of two things will occur.
- The pushing force will exceed the maximum static friction force, and the box will begin to slide across the surface (slipping).
- Or, the pushing force and the friction force will create a strong enough couple that the box tip on its corner (tipping).
Free body diagram of a box pushed by a horizontal force (\(P\)) with a variable weight \(W\text{,}\) height, angle, pushing force \(P\text{,}\) and coefficient of static friction \(\mu_\text{s}\text{.}\) Under varying conditions, the box will either tip, slip, or stay static.
One of the most straightforward ways to determine how the box will move is to solve for the pushing force twice, once assuming slipping and a second time expecting tipping. Whichever iteration requires the least pushing force is the option that will cause the box to move. This process is summarized in the following three steps:
This process is summarized in the following three steps:
-
Check slipping.
Create an FBD with the normal force \(N\) at some unknown location and solve for the pushing force necessary to make the body slip.
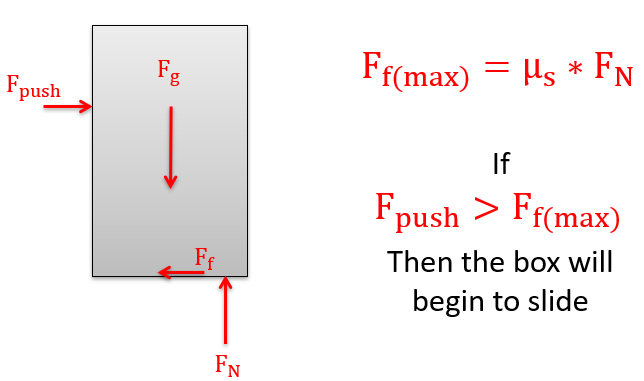
Figure 9.3.2. A body will slide across a surface if the pushing force exceeds the maximum static friction force that can exist between the two surfaces in contact. As in all dry friction problems, this limit to the friction force is equal to the static coefficient of friction times the normal force between the body (\(F=\mu_\text{s} N\)). Given the scenario below of a box on a horizontal surface, if the pushing force exceeds the maximum force of friction, then the body will slip. -
Check tipping.
Create an FBD with the normal force \(N\) at the corner of the box and solve for the pushing force necessary to make the body tip.
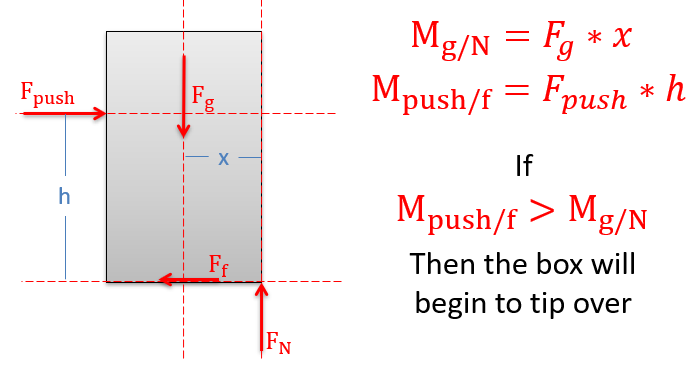
Figure 9.3.3. Given the box on a rough horizontal surface above, as we push horizontally on the body, the resultant normal force (as discussed above in section XX) will shift to the right. Because the normal force is the direct result of physical contact, we cannot move the normal force beyond the corner of the box. At tipping, the friction force is static-but-not-impending as it has not reached impending motion for slipping. -
Compare the results.
In this case, the least value of \(F_\text{push}\) will initiate impending motion.