statics Simple Trusses

Section 6.2 Simple Trusses

Key Questions

At the end of this chapter you should be able to answer these questions.

What are simple trusses and how do they differ from other structural systems?
What are the benefits and dangers of simple trusses?
How can we determine the forces acting within simple truss systems?
For a truss in equilibrium, why is every individual member, joint, and section cut from the truss also in equilibrium?
How do we identify zero-force members in a truss and use their presence to simplify the analysis?

Subsection 6.2.1 Overview of Simple Trusses

Simple trusses are made purely of straight two-force members, connected with frictionless pins, and organized into triangles. Simple trusses, by definition, are statically determinate, having a sufficient number of equations to solve for all unknowns values. While the members of real-life trusses stretch and compress under load, we will continue to assume that all bodies we encounter are rigid.

When analyzing trusses, we are looking to identify the axial forces acting within each member for a given loading. In mechanics classes taken after statics, you will be able to use these axial forces to select a material and design the cross sectional properties of each member. Later in Ch 8: Internal Loading within Rigid Bodies chapter of this book, you will analyze additional internal loadings in members, including shear force and bending moment.

It is worth various types of forces that you will encounter on truss free-body diagrams. These are the forces you need to consider in truss systems. Since a truss system contains only two-force members, there will be no moments involved.

Applied Forces: Applied forces are the external forces which a rigid body or system of rigid bodies is being designed to support. They are often given in a problem and you will be asked to find the reaction and interaction forces developed by them.
Body Forces: Body forces are gravitational weight forces of rigid bodies within a system. To maintain the assumption that trusses are formed of two-force members, all included weight forces must be split in two and distributed to the pins on either end of a truss member.
Reaction Forces: Reaction forces come from support pins, support rollers, or support two-force members interacting with the outside world.
Interaction Forces: Interaction forces are caused by the connection of one body with all the others it touches. Hence, when looking at the force on a pin joint, we would include all the forces coming from all members and reactions connected to that pin joint.
Internal Forces: Internal forces are the forces developed within the members of a truss. For trusses with straight members, the internal forces are compression and tension.

Thinking Deeper: The Danger of Simple Trusses.

Simple trusses have no structural redundancy, which makes them easy to solve using the techniques of this chapter, however this simplicity also has a dark side.

These trusses are sometimes called fracture critical trusses because the failure of a single component can lead to catastrophic failure of the entire structure. With no redundancy, there is no alternative load path for the forces that normally would be supported by that member. You can visualize the fracture critical nature of simple trusses by thinking about a triangle with pinned corners. If one side of a triangle fails, the other two sides lose their support and will collapse. In a full truss made of only triangles, the collapse of one triangle starts a chain reaction which causes others to collapse as well.

While fracture critical bridges are being replaced by more robust designs, there are still thousands in service across the United States. To read more about two specific fracture critical collapses search the internet for:

Silver Bridge Collapse Ohio River
I-5 Bridge Collapse Skagit River

Subsection 6.2.2 Identifying Simple Trusses

As discussed in Table 6-1 there are some rules which separate simple trusses from other systems of rigid bodies.

Simple trusses are made of all two-force members and all joints are modeled as frictionless pins. All applied and reaction forces are applied only to these joints.
Simple trusses are made of triangles, which makes them rigid when removed from supports. Simple trusses are determinate, having a balance of equations and unknowns, following the equation:
\begin{equation*} \underbrace{2\times (\text{number of joints})}_{\text{system equations}} = \underbrace{(\text{number of reaction forces}) + (\text{number of members})}_{\text{system unknowns}} \end{equation*}

A few additional notes include:

Commonly, rigid trusses have only three reaction forces, resulting in the equation:
\begin{equation*} 2\times (\text{number of joints})=3 + (\text{number of members}) \end{equation*}
Unstable trusses lack the structural members to maintain their rigidity when removed from their supports. They can also be recognized using the equation above having more system equations on the left side of the equation above then system unknowns on the right.
Truss systems with redundant members have fewer system equations on the left side of the equation above than the system unknowns on the right. While they are indeterminate in statics, in later courses you will learn equations to solve for member stretching and compression you will gain more equations for these trusses can be solved

Exposed vs. Unexposed Internal Forces.

Cutting a straight member in a truss exposes the internal force which must be properly represented on the free-body diagram. Internal forces of a truss are all in equal and opposite pairs, think about the tension forces in a two-force member being equal and opposite pulling on each end. Hence, all interaction and internal forces which are not exposed by cutting or isolating members have an opposing force which effectively cancels them out. Only when we cut through a member or joint in the isolation step of creating a free-body diagram, do we expose all the forces which come from the interaction of the surrounding bodies.

Subsection 6.2.3 Solving Trusses

“Solving” a truss means identifying and determining the unknown forces carried by the members of the truss when supporting the assumed load. This is only the first step of a thorough analysis of a truss structure. Later steps would include refining the initial analysis by considering other load conditions, accounting for the weight of the members, relaxing the requirement that the members be connected with frictionless pins, and ultimately determining the stresses in the structural members and the dimensions required in order to prevent failure.

Two major strategies to solve trusses will be covered in the following sections: the Method of Joints and the Method of Sections. Either method may be used, but the Method of Joints is usually easier when finding the forces in all the members, while the Method of Sections is a more efficient way to solve for specific members without solving the entire truss. It’s also possible to mix and match methods when necessary.

The first steps to solve a truss are the same regardless of the method you choose.

First, ensure that the structure can be modeled as a simple truss, then draw and label a sketch of the entire truss. Each joint should be labeled with a letter, and the members will be identified by their endpoints, so member \(AB\) is the member between joints \(A\) and \(B\text{.}\) This will help you keep everything organized and consistent in later analysis.

Then, treat the entire truss as a rigid body and solve for the external reactions using the methods of Chapter 5. If the truss is cantilevered and unsupported at one end you may not actually need the reaction forces and may skip this step. The reaction forces can be used later to check your work.

Figure 6.2.1. Truss Labels.

Figure 6.2.2. Free body diagram.

Subsection 6.2.4 Zero-Force Members

Sometimes a truss will contain one or more zero-force members. As their name implies, zero-force members carry no force and thus support no load. Zero-force members can be found by applying equilibrium equations to the joints at either end of a member, but you can save yourself some work if you can find and eliminate them before you begin. Fortunately, zero-force members can easily be identified by inspection with two simple rules.

Rule 1: If two non-collinear members meet at an unloaded joint, then both are zero-force members.
Rule 2: If three forces (interaction, reaction, or applied forces) meet at a joint and two are collinear, then the third is a zero-force member.

Consider the truss to the left. Assume that the dimensions, angles and the magnitude of force \(C\) are given. At joint \(B\text{,}\) there are two vertical collinear members as well as a third member which is horizontal, so Rule 2 should apply.

What does Rule 2 say about member \(BD\text{?}\) Can it tell us anything about member \(DA\text{?}\)

Cutting the members at the dotted boundary line exposes internal forces \(BC\text{,}\) \(BD\) and \(BA\text{.}\) These forces act along the axis of the corresponding members by the nature of two-force members, and for convenience have been assumed in tension although that may turn out to be incorrect.

Rule 2 applies here since \(BA\) and \(BC\) are collinear and \(BD\) is not.

The free-body diagram of joint \(B\) may be drawn by eliminating the cut members and only showing the forces themselves.

The situation is simple enough to apply the equilibrium equations in your head.

Vertically, forces \(BC\) and \(BA\) must be equal, and horizontally, force \(BD\) must be zero to satisfy \(\Sigma F_x = 0\text{.}\) We learn that member \(BD\) is a zero-force member.

While it is probably easiest to think about Rule 2 when the third member is perpendicular to the collinear pair, it does not have to be. Any perpendicular component must be zero which implies that the corresponding member is zero-force.

Continuing the analysis at joint \(D\) draw its free-body diagram. Keep in mind that if one end of a member is zero-force the whole member is zero-force. Since member \(BD\) is zero-force, horizontal force \(BD\) acting on joint \(D\) is zero and need not be included on the free-body diagram, and the remaining three forces match the conditions to apply Rule 2.

Analyzing the joint as before, but with a coordinate system aligned with the collinear pair,

\begin{align*} \Sigma F_y \amp = 0\\ - DA_y \amp = 0\\ DA \sin \theta \amp = 0 \end{align*}

This equation will be satisfied if \(DA = 0\) or if \(\sin \theta = 0\) but the second condition is only true when \(\theta = \ang{0}\) or \(\theta =\ang{90}\text{,}\) which is not the case here. Therefore, force DA must be zero, and we can conclude that member DA is a zero-force member as well.

Finding zero-force members is an iterative process. If you determine that a member is zero-force, eliminate it and you may find others.

Finally consider joint \(C\) and draw its free-body diagram. Does either Rule apply to this joint? No. You will need to solve two equilibrium equations with this free-body diagram to find the magnitudes of forces \(CD\) and \(CB\text{.}\)

On the other hand, if the horizontal load \(C\) was not present, then Rule 1 would apply and both members \(BC\) and \(DC\) would be zero-force.

The final truss after eliminating the zero-force members is shown to the left. Forces \(BC=BA\) and \(DC = DE\) and the members may be replaced with longer members \(AC\) and \(CE\text{.}\)

The original truss has been reduced to a simpler triangular structure with only three internal forces to be found. Once you are able to spot zero force members, this simplification can be made without drawing any digrams or performing any calculations.

Thinking Deeper: Why include Zero-Force Members?

You may be wondering what is the point of including a member in a truss if it supports no load. In our simplified example problems, they really are unnecessary, but in the real world, zero-force members are important for several reasons:

We have assumed that all members have negligible weight or if not, applied half the weight to each pin. The actual weight of real members invalidates the two-force body assumption and leads to errors. Consider a vertical member -- the internal forces must at a minimum support the weight of the member.
Truss members are not actually rigid, and long slender members under compression will buckle and collapse. The so-called zero-force member will be engaged to prevent this buckling. In the previous example, members CD and DE are under compression and form an unstable equilibrium and would definitely buckle at pin \(D\) if they were not replaced with a single member \(CE\) with sufficient rigidity.
Trusses are often used over a wide array of loading conditions. While a member may be zero-force for one loading condition, it will likely be engaged under a different condition — think about how the load on a bridge shifts as a heavy truck drives across.

So finding a zero-force member in a determinate truss does not mean you can discard the member. Zero-force members can be thought of as removed from the analysis, but only for the loading you are currently analyzing. After removing zero-force members, you are left with the simplest truss which connects the reaction and applied forces with triangles. If you misinterpret the rules you may over-eliminate members and be left with missing legs of triangles or ‘floating’ forces that have no load path to the foundation.

Example 6.2.1. Zero-Force Member Example.

Given the truss below, eliminate all the zero-force members, and draw the remaining truss.

Answer

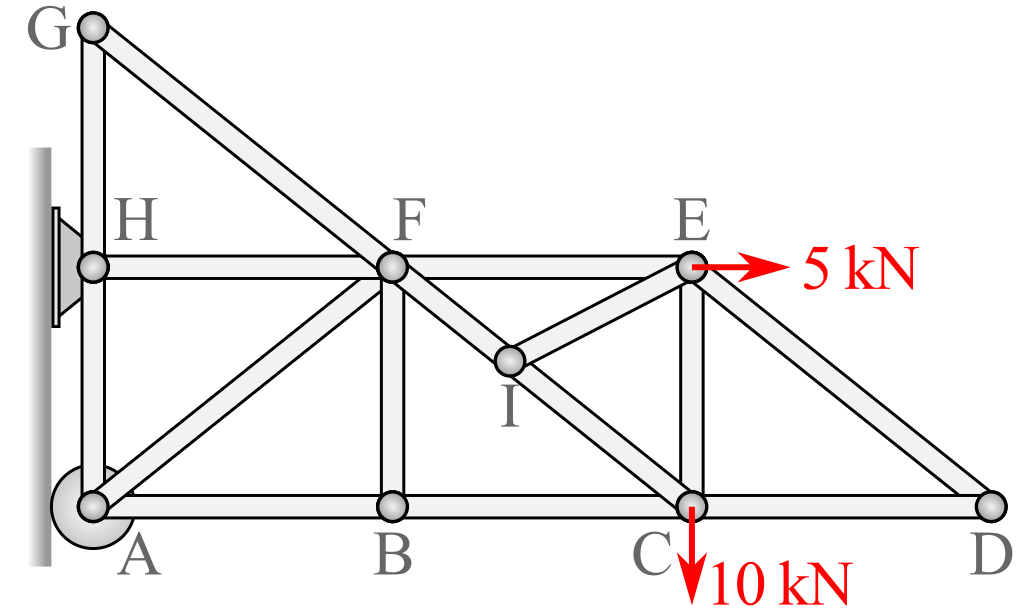
There are six zero-force members: \(GH\text{,}\) \(FG\text{,}\) \(BF\text{,}\) \(EI\text{,}\) \(DE\) and \(CD\text{.}\)

Solution

Rule 1:

Due to two members meeting at unloaded joint \(G\text{,}\) both members \(GH\) and \(FG\) are zero-force members
Due to two members meeting at unloaded joint \(D\text{,}\) both members \(DE\) and \(CD\) are zero-force members

Rule 2:

Due to three forces meeting at joining \(B\text{,}\) with two being collinear (internal forces in \(AB\) and \(BC\)) then \(BF\) is a zero-force member.
Due to three forces meeting at joint \(I\text{,}\) with two being collinear (internal forces \(IF\) and \(CI\)), then \(EI\) is a zero-force member. Note that member \(EI\) does not need to be perpendicular to the collinear members to be a zero force.

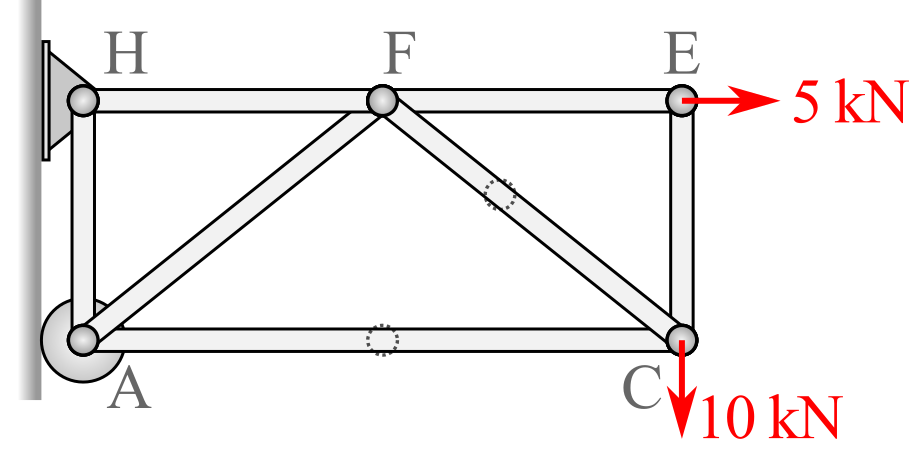
The remaining truss is shown. Note that once \(EI\) and \(BF\) are eliminated, you can effectively eliminate the joints \(B\) and \(I\) as the member forces in the collinear members will be equal. Also notice that the truss is still formed of triangles which fully support all of the applied forces.

Try to find all the zero-force members in the truss in Figure 6.2.3 below, once you believe you have found all of them, check out the step-by-step solution in the interactive.

Figure 6.2.3. This interactive will allow you to see the full and iterative evaluation of zero-force members, including both Rule 1 and Rule 2, on the included truss.