Section 6.5 Frames and Machines
Key Questions
At the end of this chapter you should be able to answer these questions.
- How are frames and machines different from trusses?
- Why can the method of joints and method of sections not be used for frames and machines?
- How do we identify if a structure is independently rigid?
- How do we apply equilibrium equations to each member of the structure, and ensure that the sense of a force appearing on multiple free-body diagrams is consistent?
Subsection 6.5.1 Frames and Machines
Frame and machines are engineering structures that contain at least one multi-force member. As their name implies, multi-force members have more than two points of application of point loads, distributed loads present and/or couples applied to them and therefore are not two-force members. Note that all bodies we investigated in Ch 5 Equilibrium of Rigid Bodies were all multi-force bodies. Refer to Table 6-1 for the details of how frames and machines compare to other equilibrium systems.
By definition:
Frames are rigid, stationary structures designed to support loads, and must include at least one multi-force member.
Machines are non-rigid structures where the parts can move relative to one another. Generally they have an input and an output force and are designed produce a mechanical advantage. Note that all machines in this text are in static equilibrium by given their interacting and applied forces.
Though there is a design difference between frames and machines they are grouped together because they can both be analyzed using the same process, which is the subject of this section.


Analyzing a frame or machine means determining all applied, reaction, and internal forces and couples acting on the structure.
The method used to analyze frames involves disassembling the structure into individual rigid bodies; we “take the structure apart.” and analyze each part separately. Each component is analyzed as an independent rigid body. This leads to equilibrium equations for each component, and due to Newton’s Third Law, every interaction force and couple is one half of a complementary pair. The interacting force of body \(A\) on \(B\) is equal and opposite to the force of body \(B\) on body \(A\) and the free-body diagrams must reflect this.
Remember from Chapter 5 Rigid Body Equilibrium how you were limited to three linearly independent equations per rigid body free-body diagram? It turns out that the relationship still holds here, but now we have more free-body diagrams to use. Here’s a few more details on the number of equations that come from each type of two-dimensional free-body diagram:
- Two-force members. One equation: Recall that two-force members can be recognized as either a cable or a weightless link with all forces coming from two frictionless pins. The available equation simply tells you that the force at one pin is equal and opposite to the force on the other placing the body in tension or compression.
- Multi-force rigid body with concurrent forces. Two equations: These are the same type of problems you solved in Ch. 3: Equilibrium of Particles with only two equations available \(\Sigma F_x = 0\) and \(\Sigma F_y = 0\text{.}\)
- Multi-force rigid body with offset forces and/or couples. Three equations: These are the most general body types where you can use \(\Sigma F_x = 0\text{,}\) \(\Sigma F_y = 0\text{,}\) and\(\Sigma M = 0\) to solve for three unknowns.
Subsection 6.5.2 Analysis Procedure
The process used to analyze frames and machines is outlined below:
-
First, determine if we can model the entire structure as a rigid body.
To do this, the structure needs to be independently rigid. This means that it would be rigid even if we separated it from its supports. Look for triangles formed among the members, as triangles are inherently rigid.
If the structure is independently rigid, you will be able to model the structure as a single rigid body to determine the reaction forces acting on the structure. If the structure is not independently rigid then skip this step.
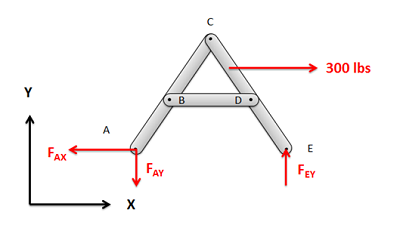
Figure 6.5.3. If, and only if, the structure is independently rigid, you should analyze the whole structure as a single rigid body to solve for the reaction forces. Note the triangle formed between pins \(B\text{,}\) \(C\text{,}\) and \(D\text{.}\) -
Next draw a free-body diagram for each of the members in the structure. You will need to include all forces acting on each member, including:
- All applied forces/couples that may be acting at the members.
- Interaction forces from two-force members. Recall, at connection points with two-force members there will be single force of unknown magnitude but the known direction (the forces will act along the line between the two connection points on the member).
- Next, add in the remaining reaction forces/couples at the connection points between members. For forces with an unknown magnitude and direction (such as in pin joints) the forces are often drawn in as having unknown x and y components.
Remember that the interaction forces/couples between connected bodies will be equal and opposite.
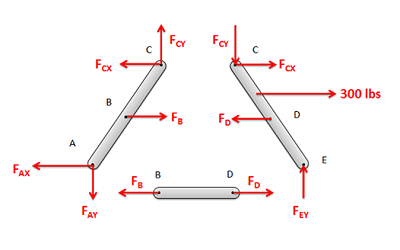
Figure 6.5.4. Separate the structure into individual components and draw a free-body diagram of each component. It is important to remember that the forces at each connection point are equal and opposite. Write out the equilibrium equations for each free-body diagram.
Finally, solve the equilibrium equations for the unknowns. You can do this algebraically, solving for one variable at a time, or you can use matrix equations to solve for everything at once. If your algebra tells you that any force/couple is negative, that indicates that the assumed direction of that term should be flipped in direction.
Thinking Deeper: Why does the Method of Joints work on trusses but fail on Frames and Machines?
We can solve trusses using the methods of joints and method of sections because all members of a truss are considered to be two-force bodies. Cutting a truss member exposes an internal force which has an unknown scalar magnitude, but a known line of action. The force acts along the axis of the member, and causes no bending if the member is straight. Cutting a truss member exposes one unknown.
Frames and machines are made of multi-force members and cutting these, in general, exposes:
- A force with an unknown magnitude acting in an unknown direction.
- A bending moment at the plane of the cut.
Cutting a two-dimensional multi-force member exposes three unknowns, and six are exposed for a three-dimensional body. The number of unknowns quickly eclipses the available equations rendering the problem impossible to solve.
Bottom line: use method of sections and joints only for trusses made of two-force straight members; for all other multi-force rigid body systems, draw and analyze free-body diagrams of the components.