Engineering Statics

Section 4.1 Introduction

When a force is applied to a body, it can have the tendency to move the body in the direction of the force (translation) and rotate the body about an axis. We have already explored the translational tendency of forces in Chapters 2 and 3, and will focus on this rotational tendency of forces here in Chapter 4. This rotational tendency is known as the moment of the force, or more simply referred to simply as the moment. Moments and torques are the exact same thing. Physicists commonly use the term torque while engineers often use the term moment.

All moments are vectors and are computed around a specific point, therefore we use the notation\(\vec{M_A}\) for the moment vector around point A. One common situation where you may have encountered moments is when you tighten or loosen a bolt with a wrench. When a force \(\vec{F}\) is applied to the wrench, as shown in Figure AA below, one effect of the applied force is to rotate the wrench with moment \(\vec{M_A}\) about an axis passing through the centerline of the bolt at A.

When working with moments, it is important to remember that moments are vectors. That is, they have both a magnitude and a direction. As such, they obey all rules of vector addition and subtraction described in Chapter 2 Forces and Other Vectors. They also have a point of application, although it is more accurate to say that moments have an axis of rotation. In two dimensions, moments will rotate about the axis perpendicular to the two-dimensional plane (hence the axis will be perpendicular to the screen/page) and so will appear to act around a point. In three dimensions, the axis of rotation can be going in any direction.

Like forces, moments have a positive and negative direction. Since moments are rotational, they may also be referred to by their direction of rotation: clockwise or counterclockwise. Using the right-hand rule convention, counter-clockwise moments are positive and clockwise moments are negative. As shown in figure BB and CC below, there are multiple ways to use your right hand to determine the sign of a moment. They all produce the same answer, so you don’t need to learn all techniques, but make sure you find one of them which you can use accurately and consistently.

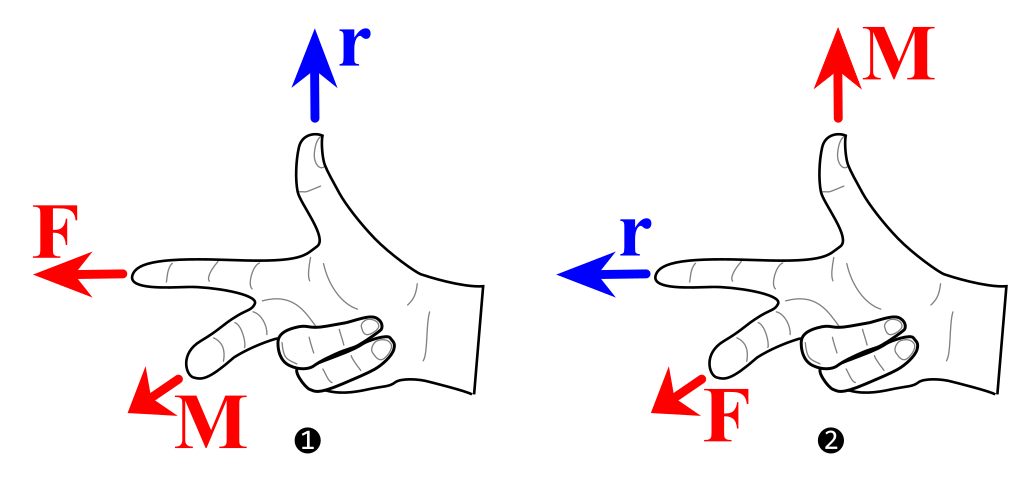
You can use the three-finger right-hand rule technique to find the direction of the moment in two different ways. As shown on the left in ❶, you can align the position vector \(\vec{r}\) with your thumb, force vector \(\vec{F}\) with your index finger, and your middle finger will then be the positive axis around which \(\vec{M}\) is rotating. As shown on the right in ❷, you can align the position vector \(\vec{r}\) with your index finger, the force vector \(\vec{F}\) with your middle finger, and your thumb will then be the positive axis around which \(\vec{M}\) is rotating.

An alternate to the three-finger right-hand rule technique is the point-and-curl right-hand rule technique. Start with your hand flat and fingertips pointing along the position vector \(\vec{r}\) going FROM the point of interest TO the force line of action, then the force vector \(\vec{F}\) pushes fingers into a curl, and finally, your thumb axis around which the moment is rotating \(\vec{M}\text{.}\)

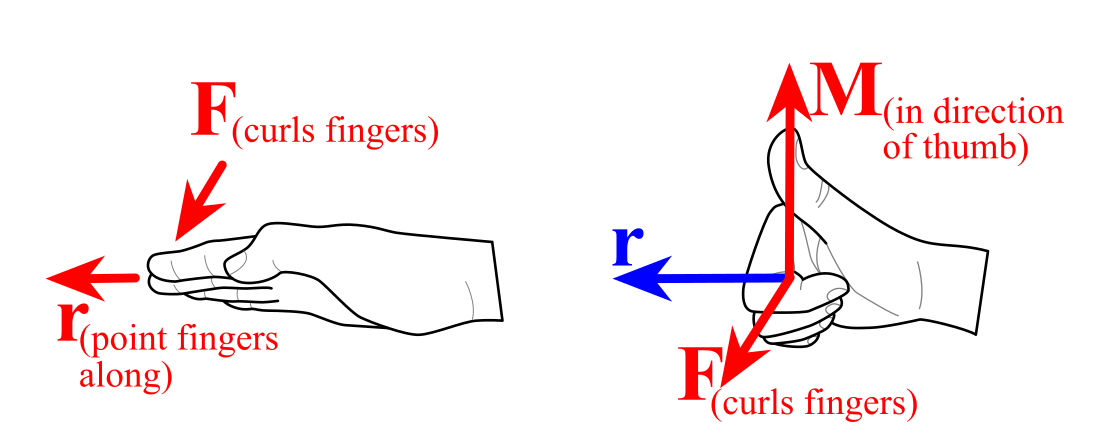
Option ❶ is \(\overrightarrow{thumb} \times \overrightarrow{index} = \overrightarrow{middle}\text{,}\) or option ❷ is \(\overrightarrow{index} \times \overrightarrow{middle} = \overrightarrow{thumb}\text{.}\)

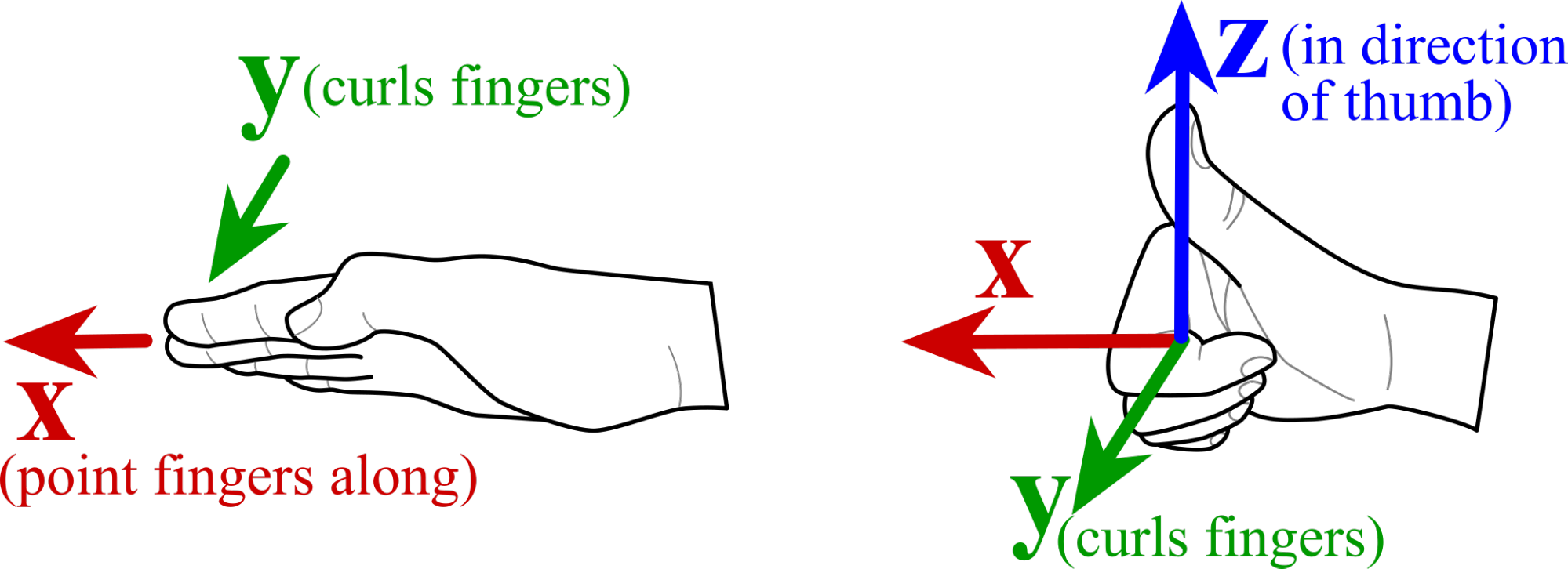
Start with fingertips sliding along the first vector \(\vec{x}\text{,}\) then the second vector \(\vec{y}\) pushes fingers into a curl, and finally, your thumb defines the direction of the final vector \(\vec{z}\text{.}\) This technique is useful for both crossing linear vectors and also determining the rotational vector direction.