statics Dry Friction

Section 9.1 Dry Friction

Key Questions

At the end of this chapter you should be able to answer these questions.

Contrast the types of friction covered in statics in the context of the other types of friction in existence
Know when you can use the equation \(F=\mu_\text{s} N\) and when you cannot
Graphically show how the friction and normal force vectors are related to the friction resultant vector and the friction angle at impending motion.
Locate and compute the friction angle \(\phi_\text{s}\) on a free-body diagram
Explain how a (typically) distributed normal force can be represented by a point force that moves as the distribution of a normal force shifts.

There are multiple types of friction, including:

Dry friction: the force that opposes one solid surface sliding across another solid surface
Fluid friction: the friction between layers of a viscous fluid in motion
Internal friction: the force resisting internal deformation of a solid material

Statics focuses on dry friction. By definition, dry friction always opposes the direction of motion of the contact point/surface that the friction is acting upon. Depending on the type of movement of the body, dry friction can either have the effect of opposing or causing motion.

Figure 9.1.1. Dry friction occurs between the bottom of this training sled and the grassy field. Dry friction is actually a surface force along the bottom surface of the sled which would oppose the motion of the sled sliding along the field. Also, notice that the point normal force is shown offset from the centroid of the sled. This offset is required to create rotational equilibrium given the pushing force.

Figure 9.1.2. Dry friction occurs between the rear tire and the road for this motorcycle. The dry friction force on the rear tire is in the direction the motorcycle is traveling and is what allows it to accelerate, for example on flat ground. There is also dry friction coming from the rolling resistance of the front tire, which is opposing the motion of the motorcycle.

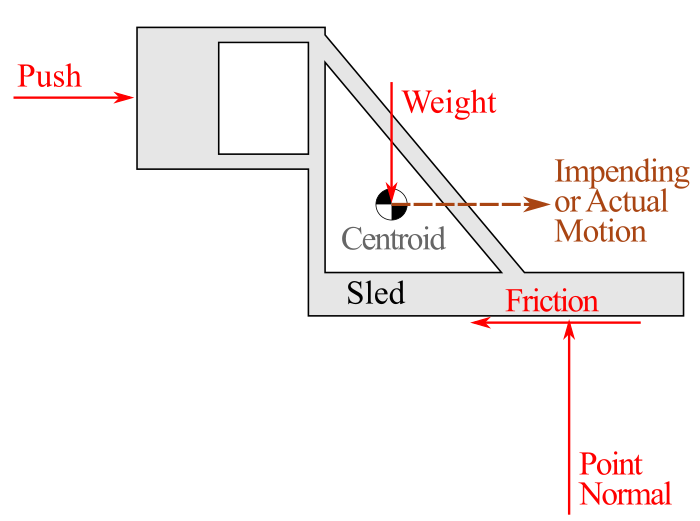
Thinking Deeper: Statically Equivalent Loadings.

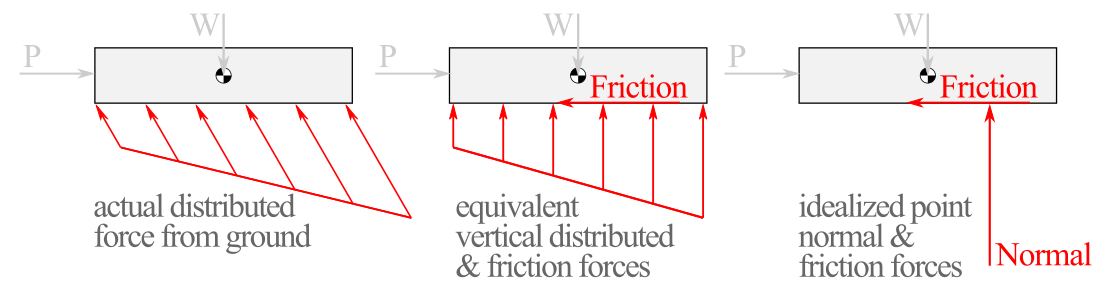
For computational simplicity, we often represent the actual force as a vertical normal force and a horizontal friction force, as shown in the third FBD below. In reality, the force acting on an object being pushed across the ground approximates the non-vertical distributed force shown in the first FBD below. The second FBD shows the intermediate step.

Subsection 9.1.1 How can you tell from a problem statement which phase of friction to use?

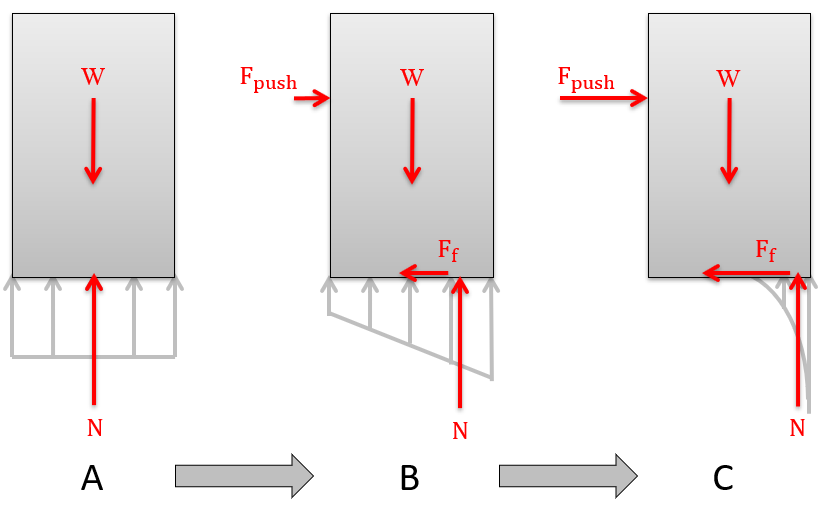
The most commonly used model for dry friction is Coulomb friction, which includes phases (as shown in Figure 9.1.3 below): (1) static but not impending friction, (2) impending motion, and (3) kinetic friction. Coulomb friction relies on a friction coefficient \(\mu\) to serve as the proportionality constant between the normal and friction forces. The friction coefficient \mu is always greater than 0 and commonly less than 1. The friction coefficient can be greater than 1 for materials that exhibit positive adhesion to each other (like silicone rubber or glued surfaces).

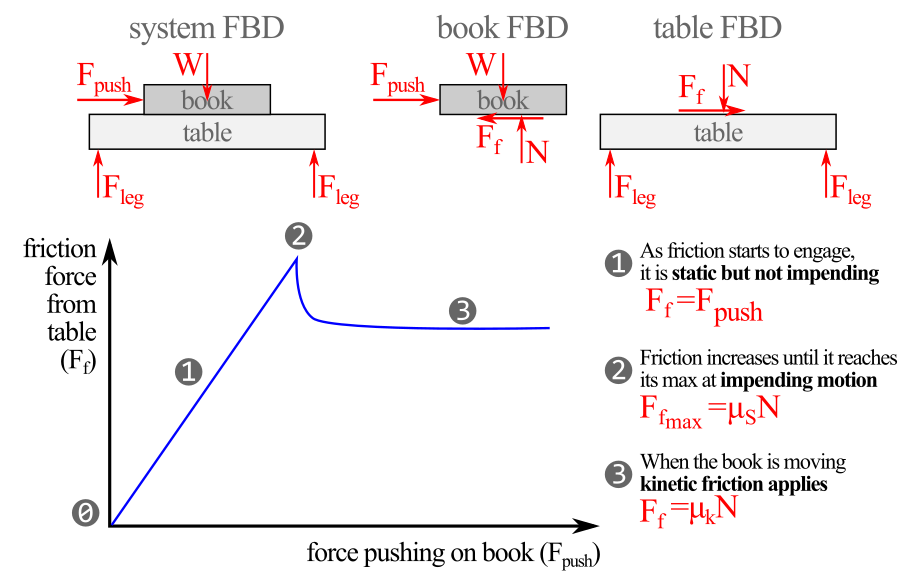
Figure 9.1.3. A simple model of a book being pushed horizontally while sitting on a table. FBDs are provided for the system, book, and table. Additionally, a Coulomb friction graph is shown and the various phases are numbered.

Here is a more detailed discussion of what happens in each friction phase.

At the origin of the graph in Figure 9.1.3, there is material interaction between the book and table, thus a friction force is available, but not engaged \(F_f=F_\text{push}=0\text{.}\)
Assuming the pushing force \(F_\text{push}\) gradually increases from zero in this static-but-not-impending phase, the friction force increases proportionally to keep the forces balanced and the box static \(F_f=F_\text{push}\text{.}\)
Next, the maximum friction possible is reached at impending motion and the pushing force matches the maximum friction force \(F_{f_\text{max}}=\mu_\text{s} N\text{.}\)
Finally, if the pushing force is increased beyond impending motion, the book starts to move under the influence of kinetic friction \(F_{f_\text{max}}=\mu_k N\text{.}\)

Notice that impending motion friction is always greater than kinetic friction, this is because the coefficient \(\mu_\text{s} \gt \mu_k\) for most materials. Practically, this tells us that once a material starts to move it is easier to keep moving than it was to get it started from rest.

If you wonder why we include kinetic friction in a statics course, remember that a body in equilibrium might be moving with constant velocity.

The key to deciding what type of friction is appropriate for a given problem will depend on the specifics of the problem statement.

Table 9.1.4. Summary of the three phases of friction with the key to recognizing and examples of each.

Type	Governing equation	Key to recognizing
Static-but-not- impending motion	None, \(F_f\) is independent of \(N\text{.}\)	Mention of sitting or static, but no extremal language
Examples: A moment of \(\Nm{20}\) is applied to a wheel held static by a brake arm. What is the friction force between the wheel and the brake arm? A box sits on a slope, find the resultant of the friction and normal forces on the box.
Impending motion	\(F_f = \mu_\text{s} N\)	The use of extremal language (related to maximum or minimum values) in the problem statements
Examples: What is the maximum force applied to the box before it will start to move? What is the minimum coefficient of static friction that will keep the box static? What is the lightest box which will not slip or tip on this slope? What is the most massive moment that the brake arm will hold static?
Kinetic friction	\(F_f = \mu_k N\)	Mention of the body moving at a constant velocity under the effect of friction. (You will learn to solve non-constant velocity friction problems in Dynamics).
Examples: A \(\kg{40}\) box is sliding down a 20° slope, what is the coefficient of friction to keep the velocity constant? A rope slips around a tree with a known friction coefficient and a constant velocity, what is the contact angle of the rope?

Note that when you solve static-but-not-impending motion problems (as opposed to impending or kinetic) that you will need one additional piece of data given in the problem to solve for both \(F_f \) and \(N\) as you will not be able to apply the equation \(F_f=\mu N\text{.}\)

Subsection 9.1.2 Friction angle and friction resultant

Friction and normal forces can be represented in two equivalent ways:

Friction and normal forces.

Using these perpendicular vectors is most convenient on block and wedge type problems and apply equally-well in all three phases of friction (static but not impending, impending motion, and kinetic friction)

Resultant force and friction angle.

Recall that resultants are the sum of two or more vectors. In this case, the friction resultant is \(\vec{R}=\vec{F}+\vec{N}\text{.}\) The friction angle \(\phi_s \) is the angle between the friction resultant and normal forces but only is applicable at impending motion. The friction resultant and friction angle are used for screw, flexible belt, and journal bearing type problems.

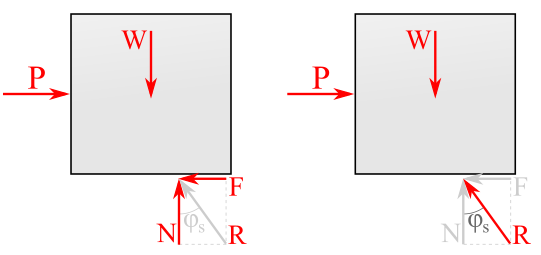
Figure 9.1.5. A block of weight \(W\) is pushed sideways by force \(P\text{.}\) The combined effect of the friction and normal forces can either be modeled as separate friction (\(F\)) and normal (\(N\)) forces (left) or a friction resultant force (\(R\)) and friction angle \((\phi_s)\text{.}\)

The friction angle \(\phi_s\) relates directly to the coefficient of static friction \((\mu_\text{s})\) as the friction angle \(\phi_s\) is the internal angle of the right triangle formed by the normal force \(N\text{,}\) the friction resultant \(R\text{,}\) and the friction force \(F\text{.}\) Hence:

\begin{equation} \tan \phi_s = \frac{F}{N} \qquad \phi_s = \tan^{-1}\left(\frac{F}{N} \right)\tag{9.1.1} \end{equation}

Subsection 9.1.3 Normal Forces

Commonly on two dimensional problems, normal forces are represented at the point of contact or in the middle of the contacting surface. However, normal forces are rarely point loads but instead are loads distributed across a surface. The point force vector we typically represent as a normal force on an FBD is the externally equivalent resultant of the distributed normal force (as demonstrated in Chapter 7, distributed loads). To demonstrate this further, take a look at Figure 9.1.6.