Section 4.6 Moments from Couples
Key Questions
At the end of this chapter you should be able to answer these questions.
- What makes a couple different than a typical \(\vec{r}\times\vec{F}\) moment?
- Why is a couple considered a pure moment?
- If a couple is applied about the point we are summing moments, does it still need to be included in the sum of moments equation?
While the moments discussed up to this point of the chapter have all been due to a single force, there is a special type of moment called a couple which is caused by a pair forces which must be 1) equal in magnitude, 2) opposite in direction, and 3) non-collinear (not sharing the same line of action). This moment is called a couple. Couples are common in mechanics and have a unique effect that the force resultant is zero, due to the equal and opposite forces. However, the sum of the moments produced by these forces is not zero. Couples, therefore, have a tendency to produce rotational motion but no translational motion. For this reason, couples are sometimes referred to as “pure moments.”
Recall that the magnitude of a moment about a point depends on the magnitude of the force and the distance between the point and the force. The magnitude of a couple about a point is independent of this distance and depends instead on the perpendicular distance between the two forces. For example, consider the scenario in Figure 4.6.1 below where two equal, opposite, and non-collinear forces form a couple on a rigid body. To calculate the magnitude of this couple about a point, we could simply calculate the moment of each force about that point and sum them together.
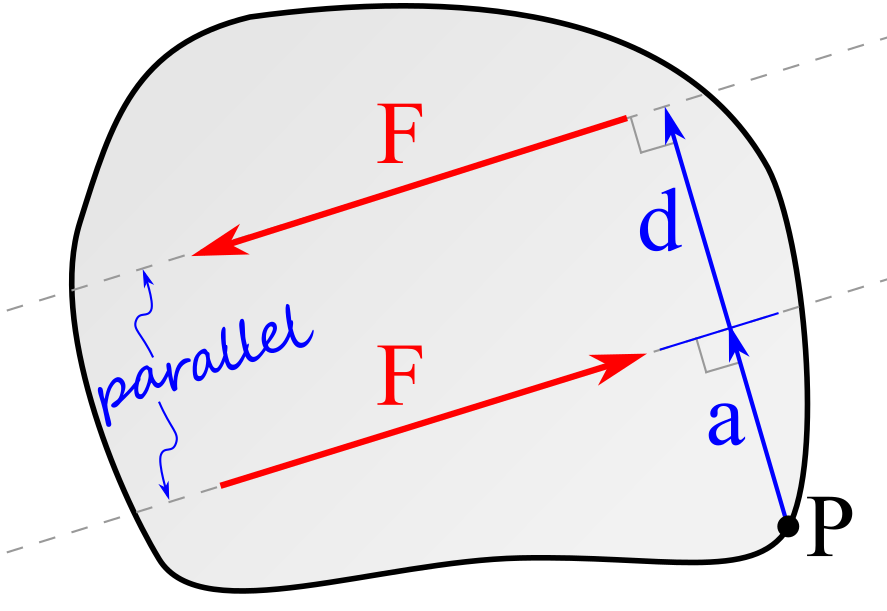
To find the resultant moment around point P we can sum the moments of each parallel force. Note that the positive and negative signs for each term in the \(\Sigma M_P \)equation come from the right-hand rule.
You will notice that \(a\text{,}\) which is the distance from the point P to the line of action of one of the forces drops out of the equation. This will happen regardless of the location of point P.
Thinking Deeper - Location independence of couples [box].
The equation above proves that couples produce the same moment at every point on the body. We can also say that the external effect of couples is location independent. Hence, no matter where you sum moments on a body, you will get the same value moment from the couple. This finding also supports the fact that if you do not recognize that a force-couple exists in a problem, simply summing the forces and moments will give you the exact same answer as resolving the force-couple into its pure moment.
We will learn in Ch 8 of this book that moving a couple around on a rigid body does affect the internal loads (or stresses) of a body, but until then we can accept that he location of a couple does not change the external loading or reactions.
In two dimensions couples are represented by a curved arrow indicating the direction of rotation. Following the right-hand rule the value will be positive if the moment is counter-clockwise and negative if it is clockwise. When you sum moments about any point on the free-body diagram, you need to include the couples in addition to all the \(\vec{r}\times\vec{F}\) moments. In equation form, we could express this as:
You can explore the computations of a couple-moment from a pair of forces in the interactive below.