Section 8.1 Internal Loads
In Subsection 3.3.3 you were introduced to axial internal loadings, loadings which were either tension or compression, or possibly zero. This section will explain two other internal loads found in two-dimensional systems, the internal shear and internal bending moment.
Internal loads are present at every point within a rigid body, but they always occur in equal-and-opposite pairs which cancel each other out, so they're not obvious. The're there however, and when an object is cut (in your imagination) into two parts the internal loads become visible and can be determined.
You are familiar with straight, two-force members which only exist in equilibrium if equal and opposite forces act on either end. Now imagine that we cut the member at some point along its length. To maintain equilibrium, forces must exist at the cut location. These forces are the internal forces and they are act in the axial direction along the long axis of the member.
In this interactive you may change the external forces on this two-force member from tension to compression, and then cut the beam into sections. You will see that each piece must have an internal force to balance the external force. If you move the cut point, you'll see that the value of the internal force is constant at every location.
Now let's examine the two-force member shown in Figure 8.1.2. This time, the member is L shaped, not straight, but the external forces must still share the same line of action to maintain equilibrium. If you cut across the object, you will obtain two rigid bodies which must also be in equilibrium. However, adding forces perpendicular to the cuts won't produce static equilibrium since the forces aren't in opposing directions. If you cut vertically and apply horizontal forces, that won't produce equilibrium either because equal and opposite forces offset like this form a couple and the pieces will rotate. This means that something is missing!
If you recall, two dimensional rigid bodies have three degrees-of-freedom and require three equilibrium equations to satisfy for static equilibrium.
\(\Sigma F_x = 0\) prevented translation in the \(x\) direction,
\(\Sigma F_y = 0\) prevented translation in the \(y\) direction, and
\(\Sigma M_z = 0\) prevented rotation.
Since we know the two halves must be in equilibrium, we must balance forces in the \(x\) and \(y\) directions and clockwise and counterclockwise moments. Assuming the material is rigid, the connection between the two halves resists both translation and rotation, so we can model this connection as a fixed support and replace the removed half of the link with a force reaction and a couple-moment reaction as shown in the free-body diagrams of Figure 8.1.3. We have resolved the force reaction into components parallel and perpendicular to the cut, and these components have special names in the context of internal loads:
The internal force component perpendicular to the cut is called the normal force. This is the same internal tension or compression force that we assumed to be the only significant internal load for trusses. If the object has an axis, and the cut is perpendicular to it, the the normal force may also be properly called an axial force.
The internal force component parallel to the cut is called the shear force. The word shear refers to the shearing between that occurs between adjacent planes due to this force. You can get a feel for shearing adjacent planes by sliding two pieces of paper together.
The internal couple moment is called the bending moment because it tends to bend the material by rotating the cut surface.
To be concise, the shear force is often simply referred to as shear, and the bending moment as moment; together with the normal or axial force the three are referred to as the “internal loading”. The symbol \(\vec{V}\) is commonly chosen for the shear force, and \(\vec{A}\text{,}\) \(\vec{P}\) or \(\vec{N}\) for the normal force.

Thinking Deeper: Resultant Loading.
The internal loadings are a simplification of what actually is a more complex loading distributed across the section plane. We can represent this complex force distribution with a single resultant force \(\vec{F}\) and couple \(\vec{M}\text{.}\) Force \(\vec{F}\) can be resolved into two orthogonal components, one parallel and the other perpendicular to the cut. The couple \(\vec{M}\) is the internal bending moment and represents the net rotational effect of the force system on the surface of the cut.
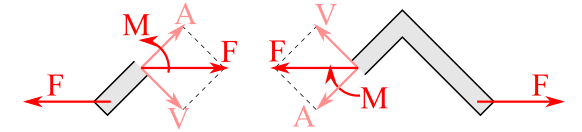
The shear force \(\vec{V}\) and normal force \(\vec{N}\) components of a force equal and opposite to \(\vec{F}\) on each FBD. The bending moment \(\vec{M}\) resists the force-couple created by the two \(\vec{F}\) forces.