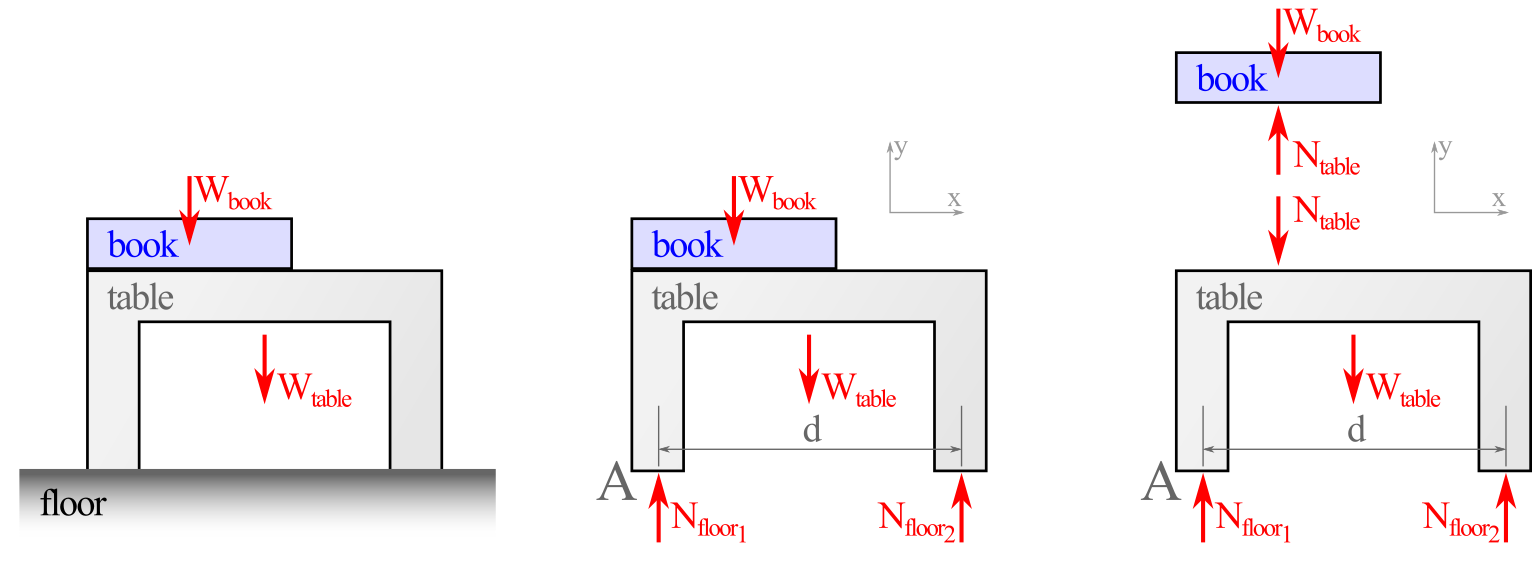
Section 1.2 Newton’s Laws of Motion
Key Questions
At the end of this chapter you should be able to answer these questions.
- What three relationships do Newton’s laws of motion define?
- What are physical examples for each of Newton’s three laws of motion?
Before jumping into Sir Isaac Newton’s Laws of Motion, let us quickly talk about motion itself. Motion can be separated into two types:
- translation
when a body changes position without rotating, and
- rotation
the spinning of a body about an axis.
Some moving bodies are purely translating or rotating, many are doing both. Conveniently, we can often isolate the translation and rotation of a body into separate equations as you will see related to Newton’s 2nd Law below.
Subsection 1.2.1 Newton’s 1st Law
Newton’s first law states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external load.
Subsubsection Application to Translational Motion
This law, also sometimes called the “law of inertia,” means that bodies maintain their current velocity unless a force is applied to change that velocity. In other words, if an object is at rest it will remain at rest until the resultant force (or net sum of forces) is out of equilibrium and changes the velocity, and if an object is moving at a constant velocity (which includes both speed and direction), it will remain at that same velocity until a force begins to change the velocity.
This rock is at rest with zero velocity and will remain at rest until a net force causes the rock to move. The net force on the rock is the sum of any force pushing the rock and the friction force of the ground on the rock opposing that force.


In the absence of friction in space, this space capsule will maintain its current velocity until some outside force causes that velocity to change.
Subsubsection Application to Rotational Motion
Newton’s first law also applies to moments and rotational velocities. A moment (or torque) is the rotational tendency of a force and you will learn much more about moments in Chapter 4. A body will maintain its current rotational velocity until a moment (applied torque) is exerted to change that rotational velocity. This can be seen in things like toy tops, flywheels, stationary bikes, and other objects that will continue spinning once started until brakes or a moment either speeds up or slows down the spinning motion.
In the absence of friction, this spinning top would continue to spin forever, but the small frictional moment exerted at the point of contact between the top and the ground will bring it to a stop eventually.

Subsection 1.2.2 Newton’s 2nd Law
Newton’s second law states that a particle accelerates in the direction of and at a rate proportional to the net applied force.
Subsubsection Application to Translational Motion
For translational motion, Newton’s 2nd law can be depicted by the equation
You will notice that the force and the acceleration are in bold face. This means that they are vector quantities, having both a magnitude and a direction. Mass on the other hand is a scalar quantity, which has only a magnitude. Both the definition and equation reflect that the magnitude of the net force is proportional to the acceleration of an object and the direction of the net force also dictates the acceleration direction of the object. As all the bodies in statics are subject to a balance of forces \(\Sigma \vec{F}=0\) it turns out that the linear acceleration \(\vec{a}\) will be equal to zero. Therefore, all bodies having no acceleration will either be at rest or remain at a constant velocity.
Subsubsection Application to Rotational Motion
Newton’s second law states that the sum of moments on an object will be proportional to angular acceleration \(\vec{\alpha}\) of the object. The proportionality constant is what is known as the mass moment of inertia of the object. In equation form this is:
Notice that the moment and the angular acceleration are vector quantities and thus have both a magnitude and direction. The mass moment of inertia, on the other hand, is a scalar quantity and has only a magnitude. Vectors and scalars will be covered in more detail in Chapter 2. As all the bodies in statics are subject to a balance of moments \(\Sigma \vec{M}=0\text{,}\) in addition to a balance of forces, it turns out that the angular acceleration \(\vec{\alpha}\) also must be equal to zero. Therefore all bodies in equilibrium are either at rest or remain at a constant angular velocity.
Subsection 1.2.3 Newton’s 3rd Law
Newton’s Third Law states “For every action, there is an equal and opposite reaction.”
The primary action Newton is referring to is a force and every force in existence comes from one body’s interaction with another body. Therefore every force on a body has an equal and opposite force which is acting on another body.
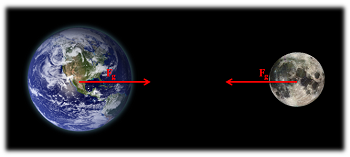
The gravitational pull of the earth and moon represent interacting bodies where the earth exerts a gravitational force on the moon, and the moon exerts an equal and opposite force on the earth.
Though there may be two equal and opposite forces acting on a single body, it is important to remember that for interacting bodies, each of the forces acts on a separate body. This can sometimes be confusing when there are multiple interacting bodies. The way to solve these multi-body systems (as discussed in the creation of Free Body Diagrams in Chapter 3 and Chapter 5), is to isolate the body or system which exposes the forces you wish to solve for.